Midterm 2 Practice Problems

Solutions will be posted under Other Content on Blackboard as we get closer to the exam.

These problems are not comprehensive, so make sure to review all of the relevant materials.

Write a recursive static method named sumReciprocals that takes as its only parameter an integer n that you can assume is positive, and that uses recursion (no loops!) to compute and return a floating-point value that is the sum of the reciprocals of the integers from 1 to n. For example, sumReciprocals(2) should return 1.5, which is 1/1 + 1/2, and sumReciprocals(4) should return approximately 2.0833, which is 1/1 + 1/2 + 1/3 + 1/4.
Write a recursive static method called removePadding() that takes a string s and that uses recursion to return a new string in which all leading and trailing spaces have been removed. For example, the call removePadding(" hello world ") should return "hello world".

A program for recursive backtracking includes a method similar to this one:

public boolean key_function(int i) {
    if (i > imax) {
        return true;
    }

    for (int alternative = 0; alternative < n; alternative++) {
        if (is_valid(alternative, i)) {
            apply_alt(alternative);
            if (_________________) {    // what goes here?
                return true;
            }
            remove_alt(alternative);
        }
    }

    return false;
}

The blank should be replaced by:

is_safe(i)
apply_alt(alternative + 1)
key_function(alternative + 1)
key_function(i)
key_function(i + 1)

Questions 4-6 involve the following method:

public static int mystery(int a[]) {
    int n = a.length;
    int result = 0;

    for (int i = 1; i < n; i++) {
        int x = a[i];        // Question 4

        int sum = 0;
        for (int j = 0; j < 3; j++) {
            sum *= a[i];     // Question 5
        }
        result += sum;

        int j = i;
        while (j > 0) {
            result += a[j];  // Question 6
            j--;
        }
    }

    return result;            
}

What is the big-O expression for the number of times that the line
```
int x = a[i];
```
is executed?
1. O(n)
2. O(n²)
3. O(n log(n))
4. O(log(n))
5. O(n!)
What is the big-O expression for the number of times that the line
```
sum *= a[i];
```
is executed?
1. O(n)
2. O(n²)
3. O(n log(n))
4. O(log(n))
5. O(n!)
What is the big-O expression for the number of times that the line
```
result += a[j];
```
is executed?
1. O(n)
2. O(n²)
3. O(n log(n))
4. O(log(n))
5. O(n!)
The following array is to be sorted using insertion sort:
```
{18, 10,  8, 35,  9, 29,  5}
```
Which of the following shows the contents of the array at the end of one of the iterations of the algorithm?
1. { 5, 10, 8, 35, 9, 29, 18}
2. { 5, 8, 9, 35, 10, 29, 18}
3. { 8, 9, 10, 35, 18, 29, 5}
4. { 8, 10, 18, 35, 9, 29, 5}
5. {10, 8, 18, 9, 29, 5, 35}
Here is an array that has just been partitioned by the first step of quicksort:
```
{3, 0, 2, 4, 5, 8, 7, 6, 9}
```
Which of the following statements is correct?
1. 5 could be the pivot, but 7 could not be.
2. 7 could be the pivot, but 5 could not be.
3. Neither 5 nor 7 could be the pivot.
4. Either 5 or 7 could be the pivot.
The following array is to be sorted:
```
{19, 22, 11, 13, 53, 34, 25}
```
Which of the algorithms that we discussed in lecture will cause the array to be ordered as follows
```
{19, 11, 13, 22, 34, 25, 53}
```
at an intermediate stage in the sorting process?
1. insertion sort
2. bubble sort
3. quicksort (with an initial pivot of 13)
4. selection sort
5. merge sort
Through experiment, you determine that selection sort performs 5000 comparisons when sorting a array of some size k. If you doubled the size of the array to 2k, approximately how many comparisons would you expect it to perform?
1. 5000
2. 10000
3. 20000
4. 40000
5. it would depend on the contents of the array
Through experiment, you determine that selection sort performs 5000 moves when sorting a array of some size k. If you doubled the size of the array to 2k, approximately how many moves would you expect it to perform?
1. 5000
2. 10000
3. 20000
4. 40000
5. it would depend on the contents of the array

Questions 12 and 13 involve linked lists of integers that are constructed from nodes whose class definition begins as follows:

public class Node {
    private int val;
    private Node next;

    public Node() {
        this.val = 0;
        this.next = null;
    }
    ...
}

You want to add a method to the Node class that takes two parameters:

a reference to the first node in a linked list (or null if the list is empty)
an integer x

The method should insert a node containing x at the front of the list, and it should return a reference to the new front of the list.

Which of these methods does this correctly?

option I:

public static Node insertFront(Node first, int x) {
    first = new Node();
    first.val = x;
    first.next = first;
    return first;
}

option II:

public static Node insertFront(Node first, int x) {
    Node n = new Node();
    n.val = x;
    n.next = first;
    return n;
}

option III:

public static Node insertFront(Node first, int x) {
    Node n = new Node();
    first = n;
    n.val = x;
    n.next = first;
    return first;
}

only I
only II
only III
I and II, but not III
II and III, but not I

The intent of the method below is to delete the last node in the linked list to which the parameter first refers:
```
public static void removeLast(Node first) {
    Node p = first;
    Node q = p.next;

    while (q.next != null) {
        p = q;
        q = q.next;
    }

    p.next = null;
}
```
Which of the following describes the subset of linked lists for which this method works correctly?
1. no linked lists
2. all nonempty linked lists
3. all linked lists with more than one node
4. the empty list and all linked lists with more than one node
5. all linked lists
A doubly linked list is constructed from nodes that are instances of the following class:
```
public class DNode {
    private char ch;
    private DNode next;
    private DNode prev;
}
```
The next field holds a reference to the next node in the linked list, and the prev field holds a reference to the previous node in the linked list.

Below is a list of three of these nodes, along with two reference variables, n and p, that refer to specific nodes in the list: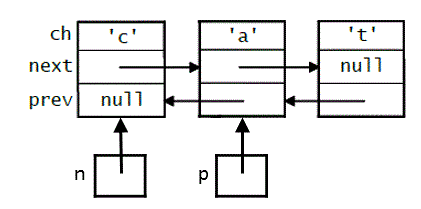

Which of the following expressions does not refer to the third node in the list?
1. p.next
2. n.next.next
3. p.prev.next
4. p.prev.next.next
5. n.next.next.prev.next
The diagram below suggests how we could implement a linked list in which we maintain a reference to both the first and last nodes in the linked list:

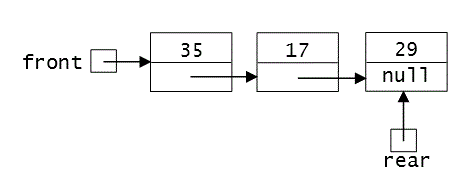
Which of the following operations would be inefficient to carry out when there are a large number of elements in the linked list?
1. insertion at the end to which front refers
2. insertion at the end to which rear refers
3. deletion from the end to which front refers
4. deletion from the end to which rear refers
The following array is to be sorted:
```
{17, 53, 71, 36, 46, 41, 23, 12}
```
1. During the execution of quicksort, what would the array look like after the first call to the partition() method?
2. During the execution of quicksort, what would the array look like after the second call to the partition() method?
3. After the initial pass of bubble sort, how would the array be ordered?
4. After three passes of selection sort, how would the array be ordered?
5. After four passes of insertion sort, how would the array be ordered?
6. During the execution of mergesort, what would the array look like after the third call to the merge() method?
The diagram below shows a linked list of characters that is constructed from instances of the StringNode class from lecture: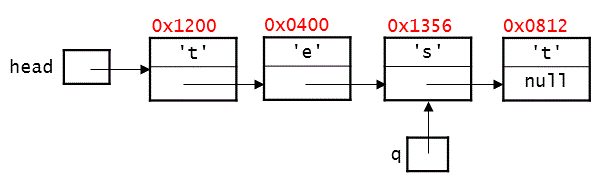

In addition, we have included two variables that each store a reference to one of the nodes in the linked list, along with the memory address of each node. You should assume that the ch field has the same address as the node itself, and that the address of the next field is 2 bytes after the beginning of the node.
1. What is the memory address of the field given by the expression head.next.next?
2. What is the value of the expression head.next.next?
3. Write one or more lines of code that remove the node containing the character 's' from the list.
4. Modify the diagram to reflect the results of executing the following lines on the original version of the list (before the 's' was removed):
```
q = q.next;
q.next = head;
```
This question involves linked lists of integers that are constructed from nodes of the following class:
```
public class Node {
    private int val;
    private Node next;
}
```
1. Write a static method named numEvenRec() that takes a reference to the first node in a linked list of integers and uses recursion to determine and return the number of even values in the list.
2. Write a static method named numEvenIter() that takes a reference to the first node in a linked list of integers and uses iteration to determine and return the number of even values in the list.
Write a static method called everyOther() that is a member of the StringNode class. It should take a reference to the first node in a linked-list string, and it should create and return a reference to a new linked-list string that contains every other character from the original string. The original linked list should not be modified. You may use either recursion or iteration.
Consider the following method:
```
public static void addAllTo(String[] names, List myList) {
    for (int i = 0; i < names.length; i++) {
        myList.addItem(names[i], i);
    }
}
```
The method takes an array of strings and an instance of one of the classes that implement the List interface from lecture – either an ArrayList or an LLList – and it adds all of the strings in the array to the list.

You may assume that the list is initially empty, and that it is possible to successfully add all of the strings in the array to the list without running out of room.

From the perspective of time efficiency, does it matter which type of List is passed in – ArrayList or LLList? Explain your answer briefly.

Last updated on February 3, 2026.