• Reinforce the point that graphs are useful modeling tools
• Review graph terminologies
• Go through proofs by contradiction and by induction

Plan:

1. Start with the historical context of Seven Bridges of Konigsberg.

The story goes like this: There were seven bridges crossing the river Pregel in the town of Konigsberg (18th century Prussia). See map and picture below. 

 

Two of the remaining bridges of Konisgsberg (now Kaliningrad in Russia). Photo is from Wikipedia.

The town people had long pondered the question of whether it is possible to walk through the town using every bridge just once, and returning home at the end.

In 1736, Euler solved the long-standing question by mapping the problem to a graph problem, which we examine next. 

2. Review the terminology for graphs

• Vertices (a.k.a. nodes)
• Edges (Directed vs undirected and labeled vs not labeled)
• Paths (and shortest paths for labeled graphs)

• Introduce the concept of node degree (number of edges incident to a vertex).

• Introduce the concept of a connected graph (a graph where there is a path from any node to any other node -- i.e., one can visit every node in the graph independent of the starting node).

• Introduce the concept of a circuit -- a path that starts in a node and ends in the same node -- possibly going through nodes multiple times.

4. The question of the town of Konigsberg was to find a circuit that traverses every edge exactly once.

Make the observation that for a circuit that traverses every edge exactly once to exist, every node must be entered and exited an equal number of times, and since no edge can be used twice, the node degree must be even.

This suggest the following conjecture.

Conjecture:  It is impossible to find a circuit that traverses all edges in a graph exactly once unless all nodes have an even degree. 

Proof: By contradiction. 

Since nodes A, B, C, and D have odd degrees, it is obvious that this cannot be done in the above graph -- putting the question of the town of Konigsberg to rest.

5. Now we ask the following question: If a connected graph satisfies the condition that all its nodes have even degree, are we guaranteed the existence of a circuit that traverses every edge exactly once?

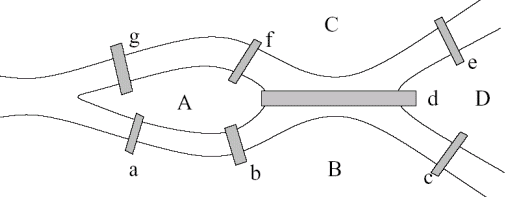
For example, to carry the story of the town of Konigsberg further, upon discovery of the above theorem (that an even degree for all nodes is a necessary condition for Eulerian circuits to exist), the town demolished the bridge from A to D and built two new bridges from C to d and from B to D, as shown below.

Now, as it turns out, it is possible indeed to cross every bridge exactly once and end up back where we started. Example: A g C e D d C f A a B c D B b A.

Trying this on a number of small graphs, one will realize that this is always possible. But is it true for all possible graphs (satisfying the above condition)? For this we need to prove the following conjecture:

Conjecture:  There exists a circuit that traverses every edge in a connected graph whose nodes are all of even degrees.

Proof: By induction. 

Base: Show that this must be the case for the graph with the smallest number of nodes -- namely three nodes in a cycle.

Step: Assume that the conjecture holds for all graphs (connected with even-degree nodes) of size less than N nodes, and consider a graph of size N.

Start in any node and follow an edge to another node. Since nodes have even degrees, I am guaranteed to exit any node I enter until I enter one of the nodes I have already visited -- call such a node X. When this happens, one of two things will happen:

1. There are edges out of X that I am yet to use. If that is the case, then keep going. 

2. There are no more edges out of X that I am yet to use. Call the circuit we obtained "C".

Under case b, we have one of two possibilities -- either:

• All edges of the graph are in C, in which case we are done since we proved the conjecture, or

• There are still some edges that are not in C. If that is the case, then consider the graph defined by the edges not in C. This graph must be of size smaller than N (since the node we stopped at cannot be part of it). Also, all nodes in this smaller graph must be of even degree. By the assumption of the induction step, we are guaranteed to find a circuit C' that traverses all edges of that smaller graph. The circuit C' can be joined to the circuit C since there must be common nodes in C and C' (otherwise the original graph would have been disconnected). Joining C and C' gives us a circuit that covers all edges of the original graph, proving the conjecture.

Azer Bestavros (2012-01-03)