Lab 10: Binary trees

Task 1: Review binary-tree basics

Your work for this task should be done on paper. Please show your work to a staff member before you leave the lab.

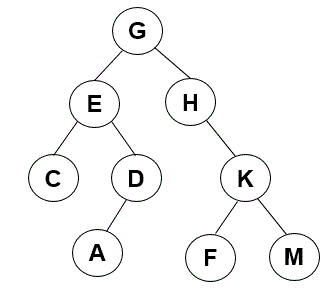
Consider the following binary tree in which the keys are letters:

1. What is the depth of node E? Of node A?

2. What is the height of the tree?

3. If a preorder traversal were used to print the keys, what would the output be?

4. What would be the output of an inorder traversal?

5. What would be the output of a postorder traversal?

6. What would be the output of a level-order traversal?

Task 2: Work with binary search trees

Your work for this task should also be done on paper.

1. Insert the following sequence of keys into an initially empty binary search tree:

   15, 23, 20, 10, 13, 6, 18, 35, 9, 24
   

2. What does the tree look like after each of the following deletions, which are carried out in sequence:

   • delete 6
   • delete 15
   • delete 20

Task 3: Work with the LinkedTree class

Download the following zip file: lab10.zip

Unzip this archive, and you should find a folder named lab10, and within it the files you will need for this lab.

1. Open LinkedTree.java in DrJava and compile it.

   Then try doing the following from the Interactions Pane:

   > LinkedTree tree = new LinkedTree();
   > tree.insert(30, "this is the root");
   > tree.insert(45, "this is one of 30's children");
   > tree.insert(15, "this is another of 30's children");
   

   Note that each call to insert() specifies two things:

   • an integer key
   • the value associated with that key (which in all of these cases is a string).

   Now try this:

   > tree.search(45)
   {this is one of 30's children}
   

   Note that the call tree.search(45) gives us back the value associated with the key 45 in the tree. More precisely, it gives us back an LLList of values associated with that key (since there could be more than one value), and the toString() method for the LLList is giving us the contents of that list surrounded by curly braces.

   Now try this:

   > tree.levelOrderPrint()
   30
   15 45
   

   Note that the levelOrderPrint() method performs a level-order traversal of the tree and prints the nodes as they are visited; each level of the tree is printed on a separate line. This method doesn’t show you the precise shape of the tree or the edges between nodes, but it gives you some sense of where the nodes are found.

2. We can use the insertKeys() method to perform a sequence of insertions in which the keys are taken from an array of integers, and the data values are strings that are based on the keys.

   For example, to create the initial tree from Task 2, we can do the following:

   > LinkedTree tree = new LinkedTree();
   > int[] keys = {15, 23, 20, 10, 13, 6, 18, 35, 9, 24};
   > tree.insertKeys(keys);
   > tree.levelOrderPrint();
   15 
   10 23 
   6 13 20 35 
   9 18 24
   > tree.inorderPrint();
   6 9 10 13 15 18 20 23 24 35
   

   Note that an inorder traversal visits the keys in order! That happens whenever your tree is a search tree.

   We can then check our answers for some of the earlier questions! For example:

   > tree.delete(6);
   > tree.delete(15);
   > tree.delete(20);
   > tree.levelOrderPrint();
   18 
   10 23 
   9 13 35 
   24
   

   Note that after these deletions, 18 is the new root node because it replaces the deleted 15. There are also other changes in the bottom two levels of the tree.

3. Let’s say that we want to compute the sum of all of the keys in a LinkedTree. Should we use recursion or iteration? Why?

4. Implement the method called sumKeysTree() whose header can be found in the LinkedTree class that we’ve given you in the lab10 folder. Read the comments to see in more detail what this method should do.

   To test this method from outside the class, you will actually need to call a separate “wrapper” method called sumKeys() that we have already implemented for you. For example:

   > LinkedTree tree = new LinkedTree();
   > int[] keys = {8, 4, 10, 2};
   > tree.insertKeys(keys);
   > tree.sumKeys()
   24
   

5. Now let’s add another method called sumAlongPath() that takes a key and uses iteration to compute and return the sum of the keys along the path from the root to the node containing the specified key. If the key is not in the tree, the method should return the sum of the keys along the path used to determine that the key is missing.

   For example, consider this search tree:

   

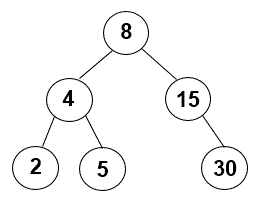
   We can create this tree as follows:

   > LinkedTree tree = new LinkedTree();
   > int[] keys = {8, 4, 15, 2, 5, 30};
   > tree.insertKeys(keys);
   

   Given this tree, here’s how your sumAlongPath() method should work:

   > tree.sumAlongPath(5)
   17
   

   Because the path from the root node to the 5 node goes from 8 to 4 to 5, the method returns 8 + 4 + 5 = 17.

   Here’s another example:

   > tree.sumAlongPath(12)
   23
   

   In an attempt to find 12, we would follow the path from 8 to 15. If 12 were in the tree, it would be in the left subtree of 15, but 15 doesn’t have a left child. Thus, the method can’t go any further, and it returns 8 + 15 = 23.

   We have given you a header for sumAlongPath() in the LinkedTree class. You should now implement this method using a loop. You may find it helpful to consult the loop used by our insert() method as a model for how you can use a loop to traverse a search tree.

Task 4: Extra questions

1. Is the tree in Task 1 a search tree? Why or why not?

2. We say that a tree is balanced when, for each node, the node’s subtrees have the same height or have heights that differ by at most one. (An empty subtree can be considered to have a height of -1.)

   Is the tree that we gave you in Task 1 balanced?

   Is the tree that results from the insertions in Task 2 balanced?

3. In Task 3.1, we performed the following insertions:

   > LinkedTree tree = new LinkedTree();
   > tree.insert(30, "this is the root");
   > tree.insert(45, "this is one of 30's children");
   > tree.insert(15, "this is another of 30's children");
   

   Does the order of the these insertions matter? Is there another ordering that would produce the same tree? What other trees could we produce if we changed the order of the insertions?

   Try to create other trees by varying the order of the insertions. Don’t forget to start by creating a new LinkedTree object before you begin each new sequence of insertions.

Task 5: Submit your work

You should show the paper with your work to the teaching assistant.

You should use Apollo to submit your modified LinkedTree.java file.

Don’t worry if you didn’t finish all of the tasks. You should just submit whatever work you were able to complete during lab.

Here are the steps:

1. Login to Apollo, using the link in the left-hand navigation bar. You will need to use your Kerberos user name and password.
2. Check to see that your BU username is at the top of the Apollo page. If it isn’t, click the Log out button and login again.
3. Find the appropriate lab section on the main page and click Upload files.
4. For each file that you want to submit, find the matching upload section for the file. Make sure that you use the right section for each file. You may upload any number of files at a time.
5. Click the Upload button at the bottom of the page.
6. Review the upload results. If Apollo reports any issues, return to the upload page by clicking the link at the top of the results page, and try the upload again, per Apollo’s advice.
7. Once all of your files have been successfully uploaded, return to the upload page by clicking the link at the top of the results page. The upload page will show you when you uploaded each file, and it will give you a way to view or download the uploaded file. Click on the link for each file so that you can ensure that you submitted the correct file.