Old version
This is the CS 112 site as it appeared on May 11, 2018.
Problem Set 4
due by 11:59 p.m. on Tuesday, February 27, 2018
Important
Don’t forget that each of your methods should be preceded by a comment that explains what your method does and what its inputs are. In addition, you should include a comment at the top of each Java file, and you should use good programming style more generally.
In addition, you should continue to follow the other guidelines that we gave you in the prior problem sets. In particular, see here and here.
Preliminaries
In your work on this assignment, make sure to abide by the collaboration policies of the course.
If you have questions while working on this assignment, please
come to office hours, post them on Piazza, or email
cs112-staff@cs.bu.edu.
Make sure to submit your work on Apollo, following the procedures found at the end of the assignment.
Part I
40 points total
Problem 1: A method that makes multiple recursive calls
10 points; individual-only
We will cover a similar problem in Lab 4 on 2/15 and 2/16.
Put all of your work for this problem in a plain-text file named
ps4pr1.txt.
A number of the algorithms that we consider in CS 112 involve recursive methods in which a given invocation of the method may make two or more recursive calls. To understand how this type of algorithm works, it helps to draw a call tree for a given set of initial parameters.
In this problem, you will draw such a call tree to illustrate the execution of a simple recursive method that operates on integers. We will cover a similar problem in Lab 4, and you may find it helpful to review our solutions to that problem before continuing.
Here is the method you will trace:
public static int foo(int x, int y) { if (y == 0) { return x; } else if (x <= y) { return y; } else { int result1 = foo(x - 1, y - 1); int result2 = foo(x - 1, y + 1); return result1 + result2; } }
Assume that we begin with the following initial call to this method:
foo(5, 3)
-
Construct a call tree that shows each invocation of the method, and that uses lines to connect a given invocation to the recursive calls that it makes (if any). Follow the same format that we use in our solutions for Lab 4, Task 1.
In particular, you should:
-
Begin by copying the following initial diagram into your
ps4pr1.txtfile:1:foo(5,3) / \ / \ / \ -
Add each subsequent call with its parameters to the call tree in the appropriate place.
-
If a given call is a base case, simply put its return value under the call, as we do in our Lab 4, Task 1 solution for calls to
fib(1)andfib(0). -
If a given call is not a base case, use lines composed of
/or\characters to connect the call to the recursive call(s) that it makes. -
Precede each call with a number that indicates the overall order in which the calls were made.
-
-
Underneath your call tree, list the order in which the calls return, as well as their return values. When you refer to a given call in this part of the problem, use its number from the call tree.
For example, the initial call always returns last, so the last line in this part of the problem should look like this:
call 1 (foo(5,3)) returns ...
where you replace the
...with its return value.See our solution for Lab 4, Task 1 for another example of what this part of your solution should look like.
Problem 2: Sum generator
16 points total; 4 points each part; individual-only
Let’s say that you want to implement a method generateSums(n) that
takes an integer n and generates and prints the results of the
following series of sums:
1 1 + 2 1 + 2 + 3 ... 1 + 2 + ... + n
For example, generateSums(4) should print the following:
1 3 6 10
and generateSums(6) should print the following:
1 3 6 10 15 21
One possible implementation of this method is the following:
public static void generateSums(int n) { for (int i = 1; i <= n; i++) { int sum = 0; for (int j = 1; j <= i; j++) { sum = sum + j; // how many times is this executed? } System.out.println(sum); } }
-
Derive an exact formula for the number of times that the line that increases the sum is executed, as a function of the parameter
n. -
What is the time efficiency of the method shown above as a function of the parameter
n? Use big-O notation as we did in lecture, and explain your answer briefly. -
Create an alternative implementation of this method that also uses iteration (i.e., you should not use recursion) but that has a better time efficiency.
-
What is the time efficiency of your alternative implementation as a function of the parameter
n? Use big-O notation as we did in lecture, and explain your answer briefly.
Problem 3: Sorting practice
14 points; 2 points for each part; individual-only
We will cover all of the sorting algorithms mentioned in this problem by Friday, February 23.
Important: When answering these questions, make sure to apply the versions of these algorithms that were discussed in lecture. The Java code for each algorithm can be found in our Sort class.
Given the following array:
{14, 7, 27, 13, 24, 20, 10, 33}
-
If the array were sorted using selection sort, what would the array look like after the third pass of the algorithm (i.e., after the third time that the algorithm performs a pass or partial pass through the elements of the array)?
-
If the array were sorted using insertion sort, what would the array look like after the third iteration of the outer loop of the algorithm?
-
If the array were sorted using insertion sort, what would the array look like after the fifth iteration of the outer loop of the algorithm?
-
If the array were sorted using Shell sort, what would the array look like after the initial phase of the algorithm, if you assume that it uses an increment of 3? (The method presented in lecture and in
Sort.javawould start with an increment of 7, but you should assume that it uses an increment of 3 instead.) -
If the array were sorted using bubble sort, what would the array look like after the second pass of the algorithm?
-
If the array were sorted using quicksort, what would the array look like after the first call to the partition method?
-
If the array were sorted using quicksort, what would the array look like after the second call to the partition method?
Important
There will be no partial credit on the above questions, so please check your answers carefully!
Part II
60 points total
Problem 4: A Sudoku solver
30 points; pair-optional
This is the only problem of the assignment that you may complete with a partner. See the rules for working with a partner on pair-optional problems for details about how this type of collaboration must be structured.
In this problem, you will write a program that solves Sudoku puzzles using recursive backtracking.
Overview
A Sudoku puzzle consists of a 9x9 grid in which some of the cells have
been filled with integers from the range 1-9. To solve the puzzle, you
fill in the remaining cells with integers from the same range, such
that each number appears exactly once in each row, column, and 3x3
subgrid.
Here is an example of an initial puzzle:
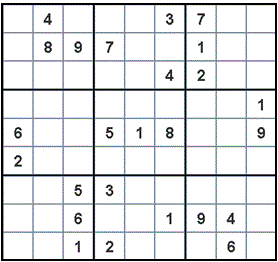
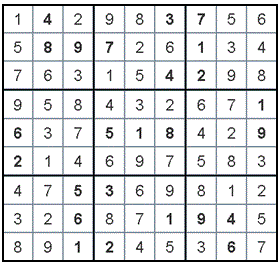
and here is its solution:
Most of the functionality of your program should go in a class called
Sudoku, which you will use to represent an individual Sudoku puzzle.
We have provided you with skeleton code for this class in the file
Sudoku.java, which you
should download and modify.
The provided code includes:
-
a field called
gridthat refers to a two-dimensional array of integers. This array will be used to store the current contents of the puzzle, such thatgrid[r][c]stores the current value in the cell at rowr, columncof the puzzle. A value of0is used to indicate a blank cell. -
a field called
valIsFixedthat refers to a two-dimensional array of booleans. It is used to record whether the value in a given cell is fixed (i.e., part of the original puzzle).valIsFixed[r][c]istrueif the value in the cell at rowr, columncis fixed, andfalseotherwise. in that cell is not fixed. For example, in the original puzzle above, there is a fixed4in the cell at row0, column1(the second cell in the top row), and thusvalIsFixed[0][1]would betruefor that puzzle. -
a field called
subgridHasValthat refers to a three-dimensional array of booleans. This array allow us to determine if a given 3x3 subgrid of the puzzle already contains a given value. For example,subgridHasVal[0][0][7]will be true if the 3x3 subgrid in the upper-left corner of the board (a subgrid that we identify using the indices[0][0]) already has a7in one of its cells. See the comments accompanying this field for information about how the subgrids are numbered. -
partial implementations of methods called
placeVal()andremoveVal()that place a value in a given cell and remove a value from a given cell by updating the fields of the calledSudokuobject. You will need to add code to these methods to update any new fields that you add. -
a full implementation of a method called
readConfig()that takes aScanneras its only parameter and reads in a initial configuration of a Sudoku puzzle from thatScanner. This method assumes that this configuration consists of nine lines of text — one for each row of the puzzle — and that each line contains nine integers separated by whitespace, with 0 used to indicate a blank cell. For example, the initial configuration of the puzzle above would begin:0 4 0 0 0 3 7 0 0 0 8 9 7 0 0 1 0 0 ...
The method reads in the puzzle configuration and updates the called object accordingly. You should not need to change this method, because it calls
placeVal(), and you are already modifying that method as needed. However, we do recommend that you read and understand this method. -
the full implementation of a method called
printGrid()that prints out the current contents of the grid belonging to the calledSudokuobject. -
the skeleton of a method called
solveRB()that you will implement. This is the key recursive-backtracking method, and it should returntrueif a solution is found to the puzzle represented by the calledSudokuobject, andfalseif no solution has yet been found (i.e., if the method is backtracking). If the initial call to this method returnsfalse, that means that the initial puzzle is not valid, and therefore no solution can be found. If there is more than one solution (which can happen if the puzzle doesn’t have enough numbers in its initial configuration), your code should stop after finding one of them.You will need to decide what parameters this method should take, and there is more than one correct choice for the number and meaning of the parameters.
Important notes:
-
Make sure that your
solveRB()method uses theplaceVal()andremoveVal()methods when updating the state of the puzzle. -
Make sure that you don’t attempt to assign a new number to cells that are filled in the original puzzle — i.e., cells whose values are fixed. Your
solve()method will need to skip over these cells somehow.
-
-
a partial implementation of a “wrapper” method called
solve()that makes the initial call tosolveRB(), and that should return the same value thatsolveRB()returns. You will need to pass in whatever initial parameter values make sense to begin the recursive-backtracking process. -
the skeleton of a constructor. You should add the code needed to initialize the additional fields that you add.
-
a
main()method that will be executed when you run your Sudoku solver. You shouldn’t need to change this method, but we encourage you to review its use of the methods of theSudokuclass. In particular, note that it displays the puzzle after the solution is found, and thus it isn’t necessary for your recursive-backtracking method to display it.
Adding fields and methods
In addition to completing the methods mentioned above, you should also
add to the Sudoku class whatever additional fields or methods are
needed to maintain the state of a Sudoku puzzle and to solve it using
recursive backtracking.
To determine what additional fields are needed, ask yourself: What other fields do I need to be able to efficiently check the constraints of the puzzle – i.e., to determine whether a given value can be placed in a given cell? Choosing appropriate fields will allow you to avoid scanning through the grid to check the constraints. See our n-Queens solver for for another example of efficient constraint checking.
Make sure that you modify the placeVal() and removeVal() methods
so that they correctly update the fields that you add. In addition,
make sure that you employ proper encapsulation.
Sample puzzles
-
no_solution.txt, which has no solution -
multi_sol.txt, which has multiple solutions
A sample run of the program is shown below.
Enter the name of the puzzle file: puzzle1.txt Here is the initial puzzle: ------------------------------------- | | 4 | | | | 3 | 7 | | | ------------------------------------- | | 8 | 9 | 7 | | | 1 | | | ------------------------------------- | | | | | | 4 | 2 | | | ------------------------------------- | | | | | | | | | 1 | ------------------------------------- | 6 | | | 5 | 1 | 8 | | | 9 | ------------------------------------- | 2 | | | | | | | | | ------------------------------------- | | | 5 | 3 | | | | | | ------------------------------------- | | | 6 | | | 1 | 9 | 4 | | ------------------------------------- | | | 1 | 2 | | | | 6 | | ------------------------------------- Here is the solution: ------------------------------------- | 1 | 4 | 2 | 9 | 8 | 3 | 7 | 5 | 6 | ------------------------------------- | 5 | 8 | 9 | 7 | 2 | 6 | 1 | 3 | 4 | ------------------------------------- | 7 | 6 | 3 | 1 | 5 | 4 | 2 | 9 | 8 | ------------------------------------- | 9 | 5 | 8 | 4 | 3 | 2 | 6 | 7 | 1 | ------------------------------------- | 6 | 3 | 7 | 5 | 1 | 8 | 4 | 2 | 9 | ------------------------------------- | 2 | 1 | 4 | 6 | 9 | 7 | 5 | 8 | 3 | ------------------------------------- | 4 | 7 | 5 | 3 | 6 | 9 | 8 | 1 | 2 | ------------------------------------- | 3 | 2 | 6 | 8 | 7 | 1 | 9 | 4 | 5 | ------------------------------------- | 8 | 9 | 1 | 2 | 4 | 5 | 3 | 6 | 7 | -------------------------------------
Problem 5: Finding pairs that sum to k
15 points total; individual-only
Suppose you are given an array of n integers, and you need to find
all pairs of values in the array (if any) that sum to a given integer
k. In a class named PairFinder, write code that performs this task
for you and outputs all of the pairs that it finds. For example, if
k is 12 and the array is {10, 4, 7, 7, 8, 5, 15}, your code should
output something like the following:
4 + 8 = 12 7 + 5 = 12 7 + 5 = 12
Note that we get two 7 + 5 sums because 7 appears twice in the array.
However, while the methods that you write may print a given
pair of values more than once in such cases, it is not necessary to do
so. In addition, the order in which the sums (and the terms within each
sum) are printed does not matter. If no pairs are found, the methods
do not need to print anything.
-
Implement a static method named
findPairSums()that requires O(n²) steps to solve this problem. The method should have the following header:public static void findPairSums(int k, int[] arr)
In addition, you should add test code for it to a
mainmethod. You may find it helpful to call therandomArray()method from ourSortCountclass to generate test arrays, although it also makes sense to use literal arrays that you define. -
Implement a static method named
findPairSumsFaster()that takes the same parameters asfindPairSums, but that requires only O(nlogn) steps in the average case to solve this problem. (Hint: you should begin by sorting the array using one of the methods from ourSortclass. Once you have done so, only O(n) additional steps are needed to find the pairs.) Here again, you should add test code to themainmethod.
Problem 6: Combining Shell sort and bubble sort
15 points total; individual-only
One of the problems with bubble sort is that it only swaps adjacent elements. In the same way that Shell sort improves on insertion sort by allowing for elements to make larger jumps, we can improve bubble sort by modifying it to operate on pairs of elements that are separated by some increment. Like Shell sort, the algorithm would begin a large increment, and successive stages of the algorithm would use smaller and smaller increments, with a final increment of 1.
In order for this approach to produce efficiency gains, we also need to modify bubble sort so that it keeps track of how many swaps that it performs during a given pass through the array. If the algorithm performs no swaps for an entire pass, or if there are no more passes to perform at that increment, the algorithm should move on to the next smaller increment. If the algorithm performs no swaps for an entire pass when the increment is 1, the algorithm terminates.
For example, consider the following array:
| 20 | 7 | 14 | 18 | 2 | 30 | 6 | 23 | 11 | 5 |
Assume that we begin with an increment of 3, which effectively divides
the array into three subarrays: {20, 18, 6, 5}, {7, 2, 23}, {14, 30,
11}. At the start of its first pass at that increment, the algorithm
compares 20 and 18 and swaps them because they are out of order with
respect to each other:
| 18 | 7 | 14 | 20 | 2 | 30 | 6 | 23 | 11 | 5 |
It next compares 7 and 2 and swaps them:
| 18 | 2 | 14 | 20 | 7 | 30 | 6 | 23 | 11 | 5 |
Then it compares 14 and 30 and does not swap them, because they are already in order with respect to each other:
| 18 | 2 | 14 | 20 | 7 | 30 | 6 | 23 | 11 | 5 |
It continues comparing and swapping as needed until it reaches the end of the array:
| 18 | 2 | 14 | 6 | 7 | 30 | 20 | 23 | 11 | 5 |
| 18 | 2 | 14 | 6 | 7 | 30 | 20 | 23 | 11 | 5 |
| 18 | 2 | 14 | 6 | 7 | 11 | 20 | 23 | 30 | 5 |
| 18 | 2 | 14 | 6 | 7 | 11 | 5 | 23 | 30 | 20 |
At this point, we know that the largest element of each subarray has bubbled to the end of its subarray. Thus, the next pass does not need to reconsider those elements–the final 3 elements of the array–on the next pass at this increment. This is similar to the way that regular bubble sort does not consider the last element on its second pass.
Here is a summary of the second pass with an increment of 3, with italics showing the elements that should not be reconsidered at this stage:
| 6 | 2 | 14 | 18 | 7 | 11 | 5 | 23 | 30 | 20 |
| 6 | 2 | 14 | 18 | 7 | 11 | 5 | 23 | 30 | 20 |
| 6 | 2 | 11 | 18 | 7 | 14 | 5 | 23 | 30 | 20 |
| 6 | 2 | 11 | 5 | 7 | 14 | 18 | 23 | 30 | 20 |
At this point, we know that the largest two elements of each subarray have bubbled to the end of their respective subarrays. Thus, the next pass does not need to reconsider those elements—the final 6 elements of the array—on the next pass at this increment. As a result, there is only one comparison/swap to perform on the third pass:
| 5 | 2 | 11 | 6 | 7 | 14 | 18 | 23 | 30 | 20 |
At this point, because the final nine elements are in the appropriate places in their subarrays, there is nothing left to do at an increment of 3, and the algorithm moves to an increment of 1, which is equivalent to regular bubble sort. However, it stops as soon as an entire pass performs no swaps.
Here’s the first pass at increment 1:
| 2 | 5 | 11 | 6 | 7 | 14 | 18 | 23 | 30 | 20 |
| 2 | 5 | 11 | 6 | 7 | 14 | 18 | 23 | 30 | 20 |
| 2 | 5 | 6 | 11 | 7 | 14 | 18 | 23 | 30 | 20 |
| 2 | 5 | 6 | 7 | 11 | 14 | 18 | 23 | 30 | 20 |
| 2 | 5 | 6 | 7 | 11 | 14 | 18 | 23 | 30 | 20 |
| 2 | 5 | 6 | 7 | 11 | 14 | 18 | 23 | 30 | 20 |
| 2 | 5 | 6 | 7 | 11 | 14 | 18 | 23 | 30 | 20 |
| 2 | 5 | 6 | 7 | 11 | 14 | 18 | 23 | 30 | 20 |
| 2 | 5 | 6 | 7 | 11 | 14 | 18 | 23 | 20 | 30 |
The second pass at that increment compares the elements in the same pairs of positions—except the final pair—but only performs one swap:
| 2 | 5 | 6 | 7 | 11 | 14 | 18 | 20 | 23 | 30 |
The third pass at that increment compares the same pairs of positions—except the final two pairs—but performs no swaps:
| 2 | 5 | 6 | 7 | 11 | 14 | 18 | 20 | 23 | 30 |
As a result, the algorithm terminates.
-
Implement this combination of Shell sort and bubble sort, adding it to the file
SortCount.java.
Your method should be as efficient as possible. In particular, it should not perform any unnecessary passes over the elements of the array, and you should not consider pairs of elements unnecessarily.Call the new method
shubbleSort. Its only parameter should be a reference to an array of integers. Like the other methods in this file, yourshubbleSortmethod must make use of thecompare(),move(), andswap()helper methods so that you can keep track of the total number of comparisons and moves that it performs. If you need to compare two array elements, you should make the method callcompare(comparison);for example,compare(arr[0] < arr[1]). This method will return the result of the comparison (true or false), and it will increment the count of comparisons that the class maintains. If you need to move elementjofarrto positioni, instead of writingarr[i] = arr[j], you should writemove(arr, i, j). -
Determine the big-O time efficiency of
shubbleSortwhen it is applied to two types of arrays: arrays that are fully sorted, and arrays that are randomly ordered. You should determine the big-O expressions by experiment, rather than by analytical argument.To do so, run the algorithm on arrays of different sizes (for example, n = 1000, 2000, 4000, 8000 and 16000). Modify the test code in the main() method so that it runs
shubbleSorton the arrays that are generated, and use this test code to gather the data needed to make your comparisons. (Note: you can also test the correctness of your method by running it on arrays of 10 or fewer items; the sorted array will be printed in such cases.)For each type of array, you should perform at least ten runs for each value of n and compute the average numbers of comparisons and moves for each set of runs. Based on these results, determine the big-O efficiency class to which shubbleSort belongs for each type of array (O(n), O(log n), O(n log n), O(n²), etc.). Explain clearly how you arrived at your conclusions. If the algorithm does not appear to fall neatly into one of the standard efficiency classes, explain your reasons for that conclusion, and state the two efficiency classes that it appears to fall between. See the section notes for more information about how to analyze the results. Put the results of your experiments, and your accompanying analysis and conclusions, in a plain-text file called
ps4pr6.txt.
Submitting Your Work
You should use Apollo to submit the following files:
- your
ps4pr1.txtfile containing your solutions for Problem 1 - your
ps4pr2.txtfile containing your solutions for Problem 2 - your
ps4pr3.txtfile containing your solutions for Problem 3 - your
Sudoku.javafile containing your solutions for Problem 4; if you worked with a partner, make sure that you each submit a copy of your joint work, and that you include comments at the top of each file specifying the name and email of your partner - your
PairFinder.javafile containing your solutions for Problem 5 - your modified
SortCount.javafile and yourps4pr6.txtfile containing your solutions for Problem 6
Warnings
-
Make sure to use these exact file names, or Apollo will not accept your files. If Apollo reports that a file does not have the correct name, you should rename the file using the name listed in the assignment or on the Apollo upload page.
-
Make sure that you do not try to submit a
.classfile or a file with a~character at the end of its name. -
Before submitting your files, make sure that your BU username is visible at the top of the Apollo page. If you don’t see your username, click the Log out button and login again.
-
If you make any last-minute changes to one of your Java files (e.g., adding additional comments), you should compile and run the file in DrJava after you make the changes to ensure that it still runs correctly. Even seemingly minor changes can cause your code to become unrunnable.
-
If you encounter problems with Apollo, click the Log Out button (if you are already logged in), close your browser, and try again. If possible, you may also want to wait an hour or two before retrying. If you are unable to submit and it is close to the deadline, email your homework before the deadline to
cs112-staff@cs.bu.edu
Here are the steps:
- Login to Apollo, using the link in the left-hand navigation bar. You will need to use your Kerberos user name and password.
- Check to see that your BU username is at the top of the Apollo page. If it isn’t, click the Log out button and login again.
- Find the appropriate problem set section on the main page and click Upload files.
- For each file that you want to submit, find the matching upload section for the file. Make sure that you use the right section for each file. You may upload any number of files at a time.
- Click the Upload button at the bottom of the page.
- Review the upload results. If Apollo reports any issues, return to the upload page by clicking the link at the top of the results page, and try the upload again, per Apollo’s advice.
- Once all of your files have been successfully uploaded, return to the upload page by clicking the link at the top of the results page. The upload page will show you when you uploaded each file, and it will give you a way to view or download the uploaded file. Click on the link for each file so that you can ensure that you submitted the correct file.
Warning
Apollo will automatically close submissions for a given file when its final deadline has passed. We will not accept any file after Apollo has disabled its upload form, so please check your submission carefully following the instructions in Step 7 above.