Lab 13: Balanced Trees; The Heap

Task 0: Complete lab evaluations

We will begin by taking a few minutes to complete evaluations for the lab component of the course.

• These evaluations are only for the teaching fellows/assistants. There is a separate evaluation of the undergraduate course assistants that you will complete as part of Problem Set 8, so please don’t comment about the CAs on today’s form.

• Your evaluations are anonymous, and we will not receive the results until after all final grades have been submitted.

• Comments in the text fields are valued and encouraged. Please try to answer all questions, but if a question is not applicable or you do not wish to answer it, you can simply skip it.

Here is the URL that you should use: bu.campuslabs.com/courseeval

• Enter your BU login name and Kerberos password, and complete the evaluation for your CS 112 lab section (the one with the section number that the TF/TA will write on the board). Please do not evaluate your lecture section at this time.

• When you are done with the survey, please close the separate browser tab.

Thanks in advance for taking the time to provide your feedback about the labs!

Balanced Trees

Recall that a binary tree is balanced if, for each of its nodes, the node’s subtrees have the same height or have heights that differ by 1. This is important because a balanced tree has a height of O(log n). Therefore, for a balanced binary search tree, the worst case for search, insert, and delete is O(h) = O(log n). Giving us the the best worst-case time complexity!

Task 1: 2-3 Trees

1. Create a 2-3 tree from the following sequence

   45, 1, 25, 12, 26, 44, 4, 50, 43, 21
   

2. Draw a new tree for each of the following operations

   • insert 5
   • insert 42

3. What numbers do I have to visit if I’m searching for

   • 44
   • 18

Heap Trees

Task 2: Review heap basics

Your work for this task should be done on paper. Please show your work to a staff member before you leave the lab.

Consider the following heap:

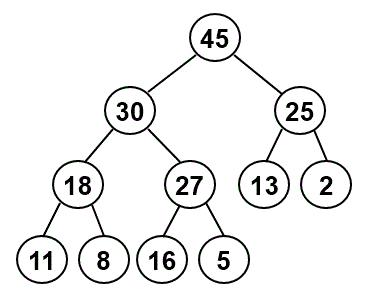
1. Which node would be in position 4 of the corresponding array?

2. Given the node in position 4, how could you use arithmetic to determine:

   • the position of its left child (if any) in the array
   • the position of its right child (if any) in the array
   • the position of its parent in the array

3. If we call the remove() method on this heap:

   • Which item will be removed?
   • Which item will be copied into the position of the removed item and then be sifted down to restore the heap?
   • What will the tree look like after this call to remove()?

4. What will the heap look like after a second call to remove()? After a third call?

5. After completing the three calls to remove(), we then use the insert() method to add an item with a key of 21. What will the tree look like after that insertion?

Task 3: Turn an array into a heap

Your work for this task should also be done on paper.

1. Consider the following array:

   {5, 3, 12, 8, 7, 4, 6}
   

   Draw the corresponding complete tree.

2. Now turn the complete tree into a heap.

   Follow the steps outlined by your lab TF.

Task 4: Heapsort

Heapsort begins by turning an array into a heap, and then it uses a sequence of heap removals to sort the array.

Each heap removal removes the largest remaining item from the heap, and the removed item is then placed in the correct position in the array – beginning with the rightmost position and working backwards from right to left.

In Task 2, you already turned an array into a heap. Now trace through the remaining steps that heapsort would take to sort that array, showing the state of the array after each new element is put into place.