Problem Set 6

due by 11:59 p.m. on Sunday, November 1, 2020

Preliminaries

In your work on this assignment, make sure to abide by the collaboration policies of the course.

If you have questions while working on this assignment, please come to office hours, post them on Piazza, or email cs112-staff@cs.bu.edu.

Part I

50 points total

Creating the necessary file

Problems in Part I will be completed in a single PDF file. To create it, you should do the following:

1. Open the template that we have created for these problems in Google Docs: ps6_partI

2. Select File->Make a copy..., and save the copy to your Google Drive using the name ps6_partI.

3. Add your work to this file.

4. Once you have completed all of these problems, choose File->Download->PDF document, and save the PDF file on your machine. The resulting PDF file (ps6_partI.pdf) is the one that you will submit. See the submission guidelines at the end of Part I.

Problem 1: Sorting practice

12 points; 2 points for each part; individual-only

Important: When answering these questions, make sure to apply the versions of these algorithms in the Sort class we give you. The Java code for each algorithm can be found in our Sort class.

Given the following array:

{10, 18, 4, 24, 33, 40, 8, 3, 12}

1. If the array were sorted using selection sort, what would the array look like after the second pass of the algorithm (i.e., after the second time that the algorithm performs a pass or partial pass through the elements of the array)?

2. If the array were sorted using insertion sort, what would the array look like after the fourth iteration of the outer loop of the algorithm?

3. If the array were sorted using the version of bubble sort presented in lecture, what would the array look like after the third pass of the algorithm?

4. If the array were sorted using the version of quicksort presented in lecture, what would the array look like after the first call to the partition() method?

5. If the array were sorted using the version of quicksort presented in lecture, what would the array look like after the second call to the partition() method?

6. If the array were sorted using the version of mergesort presented in lecture, what would the array look like after the completion of the fourth call to the merge() method—the method that merges two subarrays? Note: the merge method is the helper method; is not the recursive mSort method.

Problem 2: More Practice with big-O

12 pts. total; 4 pts. each part; individual-only

1. Determine the appropriate big-O expression for each of the following functions, and put your answer in the table we have provided in section 2-1 of ps6_partI. We’ve included the answer for the first function. (Note: We’re using the ^ symbol to represent exponentiation.)

   1.     a(n) = 5n + 1
   2.     b(n) = 5 - 10n - n^2
   3.     c(n) = 4n + 2log(n)
   4.     d(n) = 6nlog(n)+ n^2
   5.     e(n) = 2n^2 + 3n^3 - 7n

2. In the following code fragment, how many times is the count() method called as a function of the variable n? Use big-O notation, and explain your answer briefly.

   for (int i = 0; i < 3; i++) {
       for (int j = 0; j < n; j++) {
           for (int k = 0; k < j; k++) {
               count();
           }
       }
   }
   

3. In the following code fragment, how many times is the count() method called as a function of the variable n? Use big-O notation, and explain your answer briefly.

   for (int i = 0; i < n; i++) {
       for (int j = n; j > 0; j = j/2) {
           count();
       }
   }
   

Problem 3: Comparing two algorithms

6 points; individual-only

Suppose that you want to count the number of duplicates in an unsorted array of n elements. A duplicate is an element that appears multiple times; if a given element appears x times, x - 1 of them are considered duplicates. For example, consider the following array:

{10, 6, 2, 5, 6, 6, 8, 10, 5}

It includes four duplicates: one extra 10, two extra 6s, and one extra 5.

Below are two algorithms for counting duplicates in an array of integers:

Algorithm A:

public static int numDuplicatesA(int[] arr) {
    int numDups = 0;
    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] == arr[i]) {
                numDups++;
                break;
            }
        }
    }
    return numDups;
}

Algorithm B:

public static int numDuplicatesB(int[] arr) {
    Sort.mergesort(arr);
    int numDups = 0;
    for (int i = 1; i < arr.length; i++) {
        if (arr[i] == arr[i - 1]) {
            numDups++;
        }
    }
    return numDups;
}

What is the worst-case time efficiency of algorithm A in terms of the length n of the array? What is the worst-case time efficiency of algorithm B? Use big-O notation, and explain your answers briefly.

Problem 4: More practice with sorting - Quicksort

5 points; individual-only

Important: When answering these questions, make sure to apply the versions of these algorithms that are in the Sort class we give you. The Java code for each algorithm can be found in our Sort class.

Given the following array:

{14, 7, 27, 13, 24, 20, 10, 33}

1. If the array were sorted using quicksort, what would the array look like after the first call to the partition method?

2. If the array were sorted using quicksort, what would the array look like after the second call to the partition method?

Problem 5: More practice with sorting - Mergesort

6 points; 2 points for each part; individual-only

Given the following array:

{24, 3, 27, 13, 34, 2, 50, 12}

1. If the array were sorted using the version of mergesort presented in lecture, what would the array look like after the completion of the second call to the merge() method—the method that merges two subarrays? Note: The merge method is the separate helper method; is not the recursive mSort method.

2. What would the array look like after the completion of the fourth call to the merge() method?

3. The initial call to the recursive mSort() method is made from within the mergeSort() “wrapper” method. This initial call to mSort() is not a recursive call, because the method is not calling itself. Rather, all recursive calls to mSort() are made from within mSort().

   Assuming that the array has at least two elements, the initial invocation of mSort() makes two recursive calls (which in turn lead to other recursive calls, and so on). Starting with the initial array above, what would the array look like after the completion of the first of these two recursive calls?

Problem 6: First Practice with references

9 points total; individual-only

A doubly linked list consists of nodes that include two references: one called next to the next node in the linked list, and one called prev to the previous node in the linked list. The first node in such a list has a prev field whose value is null, and the last node has a next field whose value is null.

The top portion of the diagram below shows a doubly linked list of characters that could be used to represent the string "ran".

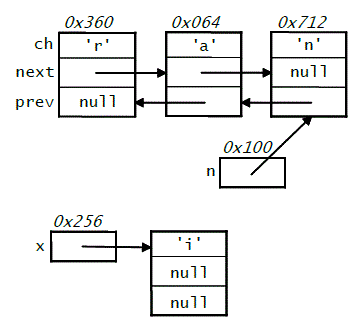
Each of the nodes shown is an instance of the following class:

public class DNode {
    private char ch;
    private DNode next;
    private DNode prev;
}

(In the diagram, we have labeled the individual fields of the DNode object that contains the character 'r'.)

In addition to the list representing "ran", the diagram shows an extra node containing the character 'i', and two reference variables: n, which holds a reference to the third node in the list (the 'n' node); and x, which holds a reference to the 'i' node. The diagram also shows memory addresses of the start of the variables and objects. For example, the 'r' node begins at address 0x360.

1. (6 points) Complete the table that we have provided in ps6_partI, filling in the address and value of each expression from the left-hand column. You should assume the following:

   • the address of the ch field of a DNode is the same as the address of the DNode itself

   • the address of the next field of a DNode is 2 more than the address of the DNode itself

   • the address of the prev field of a DNode is 6 more than the address of the DNode itself, which means that it is also 4 more than the address of the next field.

2. (3 points) Write a Java code fragment that inserts the 'i' node between the 'a' node and the 'n' node, producing a linked list that represents the string "rain". Your code fragment should consist of a series of assignment statements. You should not make any method calls, and you should not use any variables other than the ones provided in the diagram. You may assume that your code is part of the main method in the DNode class, and thus it has direct access to the private fields of the DNode objects.

   Make sure that the resulting doubly linked list has correct values for the next and prev fields in all nodes.

Submitting your work for Part I

Note: There are separate instructions at the end of Part II that you should use when submitting your work for that part of the assignment.

Submit your ps6_partI.pdf file using these steps:

1. If you still need to create a PDF file, open your ps6_partI file on Google Drive, choose File->Download->PDF document, and save the PDF file on your machine.

2. Login to Gradescope by clicking the link in the left-hand navigation bar, and click on the box for CS 112.

3. Click on the name of the assignment (PS 5: Part I) in the list of assignments on Gradescope. You should see a pop-up window labeled Submit Assignment. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

4. Choose the Submit PDF option, and then click the Select PDF button and find the PDF file that you created. Then click the Upload PDF button.

5. You should see a question outline along with thumbnails of the pages from your uploaded PDF. For each question in the outline:

   • Click the title of the question.
   • Click the page(s) on which your work for that question can be found.

   As you do so, click on the magnifying glass icon for each page and doublecheck that the pages that you see contain the work that you want us to grade.

6. Once you have assigned pages to all of the questions in the question outline, click the Submit button in the lower-right corner of the window. You should see a box saying that your submission was successful.

Part II

50 points total

Problem 7: Removing duplicates

15 points total; pair-optional

Suppose you are given an already sorted array that may contain duplicate items—i.e., items that appear more than once. In a class named Duplicates, implement a static method named removeDups() that takes a sorted array of integers and removes whatever elements are necessary to ensure that no item appears more than once.

Make your method as efficient as possible in the number of operations that it performs. In addition, your method should use O(1) additional memory—i.e., it should not create and use a second array.

The remaining elements should still be sorted, and they should occupy the leftmost positions of the array. The array locations that are unused after the duplicates are removed should be filled with zeroes. The method should return an integer that specifies the number of unique values in the array.

For example, the following test code:

int[] arr = {2, 5, 5, 5, 10, 12, 12};
int ret = removeDups(arr);
System.out.println(Arrays.toString(arr));
System.out.println(ret);

should output:

[2, 5, 10, 12, 0, 0, 0]
4

Important note: One inefficient approach would be to scan from left to right, and, whenever you encounter a duplicate, to shift all of the remaining elements left by one. The problem with this approach is that elements can end up being shifted multiple times, and thus the algorithm has a worst-case running time that is O(n²). Your method should move each element at most once. This will give it a running time that is O(n). Only partial credit will be given for methods that move elements more than once.

Problem 8: Finding pairs that sum to k

15 points total; individual-only

Suppose you are given an array of n integers, and you need to find all pairs of values in the array (if any) that sum to a given integer k. In a class named PairFinder, write code that performs this task for you and outputs all of the pairs that it finds. For example, if k is 12 and the array is initialized as: {10, 4, 7, 7, 8, 5, 15}, your code should output something like the following:

4 + 8 = 12
7 + 5 = 12
7 + 5 = 12

Note that we get two 7 + 5 sums because 7 appears twice in the array. However, while the methods that you write may print a given pair of values more than once in such cases, it is not necessary to do so. In addition, the order in which the sums (and the terms within each sum) are printed does not matter. If no pairs are found, the methods do not need to print anything.

1. Implement a static method named findPairSums() that requires O(n²) steps to solve this problem. The method should have the following header:

   public static void findPairSums(int k, int[] arr)
   

   In addition, you should add test code for it to a main method. You may find it helpful to call the randomArray() method from our SortCount class to generate test arrays, although it also makes sense to use literal arrays that you define.

2. Implement a static method named findPairSumsFaster() that takes the same parameters as findPairSums, but that requires only O(nlogn) steps in the average case to solve this problem. (Hint: you should begin by sorting the array using one of the methods from our Sort class. Once you have done so, only O(n) additional steps are needed to find the pairs.) Here again, you should add test code to the main method.

Problem 9: A merge-like approach to finding the intersection of two arrays

20 points; individual-only

In a file named MergeIntersect.java, implement a static method named intersect that takes two arrays of integers as parameters and uses an approach based on merging to find and return the intersection of the two arrays – i.e., all values that are found in both arrays.

More specifically, you should do the following:

1. Begin by creating a new array for the intersection. What should the length of this array be?

2. Use one of the more efficient sorting algorithms from Sort.java to sort both of the arrays.

3. Find the intersection of the two arrays by employing an approach that is similar to the one that we used to merge two sorted subarrays (i.e., the approach taken by the merge method in Sort.java). Your method should not actually merge the two arrays, but it should take a similar approach—using indices to “walk down” the two arrays, and making use of the fact that the arrays are sorted. As the elements of the intersection are found, put them in the array that you created at the start of the method.

   For full credit:

   • The intersection that you create should not have any duplicates.

   • Your algorithm should be as efficient as possible. In particular, you should perform at most one complete pass through each of the arrays.

4. At the end of the method, return a reference to the array containing the intersection.

5. Add test code for your method to the main method. Recall that that you can use the Arrays.toString() method to convert an array to a string; import the java.util. package to gain access to the Arrays class.

Example #1:

int[] a1 = {10, 5, 7, 5, 9, 4};
int[] a2 = {7, 5, 15, 7, 7, 9, 10};
int[] result = MergeIntersect.intersect(a1, a2);
System.out.println( result );

You should expect to see:

[5, 7, 9, 10, 0, 0]

Example #2:

int[] a1 = {0, 2, -4, 6, 10, 8};
int[] a2 = {12, 0, -4, 8};
int[] result = MergeIntersect.intersect(a1, a2);
System.out.println( result );

You should expect to see:

[-4, 0, 8, 0]

Notes:

• The array containing the intersection has the same length as the shorter of the original arrays.

• When the number of values in the intersection (call it n) is smaller than the length of the shorter array, we end up with extra 0s at the end of the array containing the intersection. This happens because the array of integers that we create is initially filled with 0s, and we only use the first n positions of the array.

Submitting your work for Part II

Note: There are separate instructions at the end of Part I that you should use when submitting your work for that part of the assignment.

You should submit only the following files:

• Duplicates.java
• PairFinder.java
• MergeIntersect.java

Make sure that you do not try to submit a .class file or a file with a ~ character at the end of its name.

Here are the steps:

1. Login to Gradescope as needed by clicking the link in the left-hand navigation bar, and then click on the box for CS 112.

2. Click on the name of the assignment (PS 5: Part II) in the list of assignments. You should see a pop-up window with a box labeled DRAG & DROP. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

3. Add your files to the box labeled DRAG & DROP. You can either drag and drop the files from their folder into the box, or you can click on the box itself and browse for the files.

4. Click the Upload button.

5. You should see a box saying that your submission was successful. Click the (x) button to close that box.

6. The Autograder will perform some tests on your files. Once it is done, check the results to ensure that the tests were passed. If one or more of the tests did not pass, the name of that test will be in red, and there should be a message describing the failure. Based on those messages, make any necessary changes. Feel free to ask a staff member for help.

   Note: You will not see a complete Autograder score when you submit. That is because additional tests for at least some of the problems will be run later, after the final deadline for the submission has passed. For such problems, it is important to realize that passing all of the initial tests does not necessarily mean that you will ultimately get full credit on the problem. You should always run your own tests to convince yourself that the logic of your solutions is correct.

7. If needed, use the Resubmit button at the bottom of the page to resubmit your work. Important: Every time that you make a submission, you should submit all of the files for that Gradescope assignment, even if some of them have not changed since your last submission.

8. Near the top of the page, click on the box labeled Code. Then click on the name of each file to view its contents. Check to make sure that the files contain the code that you want us to grade.