Problem Set 8

due by 11:59 p.m. on Sunday, November 15, 2020

Preliminaries

In your work on this assignment, make sure to abide by the collaboration policies of the course.

If you have questions while working on this assignment, please come to office hours, post them on Piazza, or email instructor.

Make sure to submit your work following the procedures found at the end of the assignment.

Part I

50 points total

Creating the necessary file

Problems in Part I will be completed in a single PDF file. To create it, you should do the following:

1. Open the template that we have created for these problems in Google Docs: ps8_partI

2. Select File->Make a copy..., and save the copy to your Google Drive using the name ps8_partI.

3. Add your work to this file.

4. Once you have completed all of these problems, choose File->Download as->PDF document, and save the PDF file on your machine. The resulting PDF file (ps8_partI.pdf) is the one that you will submit. See the submission guidelines at this specification.

Important: Put your responses to each of the following problems in the appropriate section of the ps8PartI template that you created on Google Drive.

Problem 1: Stable and unstable sorting

5 points; individual-only

Sorting algorithms can be applied to records of data, where each record consists of multiple fields. In such contexts, the sorting algorithm orders the records according to one of the fields, and the value of that field is referred to as the key of the record.

A sorting algorithm is stable if it preserves the order of elements with equal keys. For example, given the following array:

{32, 12a, 4, 12b, 39, 19}

where 12a and 12b represent records that both have a key of 12, a stable sorting algorithm would produce the following sorted array:

{4, 12a, 12b, 19, 32, 39}

Note that 12a comes before 12b, just as it did in the original, unsorted array. Insertion sort is an example of a stable sorting algorithm.

Stability can be useful if you want to sort on the basis of two different fields—for example, if you want records sorted by last name and then, within a given last name, by first name. You could accomplish this in two steps: (1) use any sorting algorithm to sort the records by first name, and (2) use a stable sorting algorithm to sort the records by last name. Because the second algorithm is stable, it would retain the order of records with the same last name, and thus those records would remain sorted by first name.

By contrast, an unstable sorting algorithm may end up reversing the order of elements with equal keys. For example, given the same starting array shown above, an unstable sorting algorithm could produce either of the following arrays:

{4, 12a, 12b, 19, 32, 39}

{4, 12b, 12a, 19, 32, 39}

Selection sort is an example of an unstable sorting algorithm. Construct an example of an input array containing two elements with equal keys whose order is reversed by selection sort. Explain why selection sort would result in an unstable sorting algorithm while insertion sort would result in a stable sort on the exact same array.

Problem 2: Choosing an appropriate implementation

12 pts. total; 4 pts. each part; individual-only

As you learned in high-school algebra, a polynomial is an algebraic expression formed by adding together terms of the form ax^b, where x is a variable and a and b are constants. a is the coefficient of the term, and b is the exponent of the term. For the sake of this problem, we will assume that all exponents are all non-negative integers. If the exponent is 0, then the term is a constant, because x⁰ = 1.

For example, the following are all examples of polynomials of the variable x:

• 6 + 5x + 8x⁵
• -2x²
• 4x³ + (-2)x⁷ + x¹²

A polynomial can be evaluated for a specific value of x by plugging in the value and computing the result. For example, when x is 2, the first polynomial above has the value

6 + 5(2) + 8(2⁵) = 6 + 10 + 8(32) = 272

One way to represent a polynomial is to store its coefficients in an array. The exponent of a given term is used to determine the position of the corresponding coefficient in the array. For example:

• 6 + 5x + 8x⁵ would be represented by the array {6, 5, 0, 0, 0, 8}

• -2x² would be represented by the array {0, 0, -2}

• 4x³ + (-2)x⁷ + x¹² would be represented by the array {0, 0, 0, 4, 0, 0, 0, -2, 0, 0, 0, 0, 1}

An alternative representation of a polynomial involves using a linked list in which each node in the list represents a single term of the polynomial. Here is one example of class that could be used for the nodes:

public class PolyNode {
    private int coeff;       // the coefficient
    private int exp;         // the exponent
    private PolyNode next;
}

The nodes would be sorted by their exponents, and it would not be necessary to include nodes for non-existent terms (i.e., terms with a coefficient of 0). For example, the linked list for the third polynomial above would look like this:

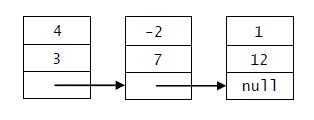
For each of the following questions, your answers should make use of big-O expressions that are functions of t, the number of terms in the polynomial, and/or m, the maximum exponent in the polynomial. (The third polynomial above has t = 3 terms and a maximum exponent m of 12.) Explain each answer briefly.

1. What is the space efficiency of each implementation?

2. What is the time efficiency of changing the coefficient of a term (e.g., changing the coefficient of the x³ term in the third polynomial from 4 to 10) in each implementation in the best, average, and worst cases?

3. What is the time efficiency of evaluating a polynomial in each implementation in the best, average, and worst cases? Important: You should assume that both implementations use a helper method that takes O(n) steps to compute x to the nth power.

4. Describe a situation in which one of the two representations would clearly be more efficient than the other one.

Problem 3: Improving the efficiency of an algorithm

13 pts. total; individual-only

The LLList.java source file can be found in the following zip folder: ps8.zip

Consider the following method, which takes two unsorted lists, list1 and list2 – both instances of class LLList – and creates a third list containing the intersection of list1 and list2:

public static LLList intersect(LLList list1, LLList list2) {
    LLList inters = new LLList();

    for (int i = 0; i < list1.length(); i++) {
        Object item1 = list1.getItem(i);
        for (int j = 0; j < list2.length(); j++) {
            Object item2 = list2.getItem(j);
            if (item2.equals(item1)) {
                inters.addItem(item2, inters.length());
                break;   // move onto the next item from list1
            }
        }
    }

    return inters;
}

The lists are unsorted, so we take a nested-loop approach in which each item in list1 is compared to the items in list2; if a match is found in list2, the item is added to the intersection and we break out of the inner loop. (Note that this method will include duplicate values in the intersection when list1 itself has duplicates; doing so is acceptable for the purposes of this problem.)

1. (3 points) What is the worst-case running time of this algorithm as a function of the length m of list1 and the length n of list2? Don’t forget to take into account the time efficiency of the underlying list operations, getItem() and addItem(). Use big-O notation, and explain your answer briefly.

2. (7 points) Rewrite this method to improve its time efficiency. Your new method should not modify the existing lists in any way, and it should use no more than a constant (O(1)) amount of additional memory. Make the new method as efficient time-wise as possible, given the constraints on memory usage. You should assume this method is not part of the LLList class, and therefore it doesn’t have direct access to the private LLList members.

3. (3 points) What is the worst-case running time of the improved algorithm? Use big-O notation, and explain your answer briefly.

Problem 4: Working with stacks and queues

10 points; 5 points each part; individual-only

1. Write a method remAllStack(Stack<Object> stack, Object item) that takes a stack and an item, and that removes all occurrences of that item from the stack. After the removals, the remaining items should still be in the same order with respect to each other. For example, if you have a stack that contains (from top to bottom) {5, 2, 7, 2, 10}, if you use the method to remove all occurrences of 2, the resulting stack should contain (from top to bottom) {5, 7, 10}.

   Important guidelines:

   • Your method may use either another stack or a queue to assist it. It may not use an array, linked list, or other data structure. When choosing between a stack or a queue, choose the one that leads to the more efficient implementation.

   • You should assume that the method does not have access to the internals of the collection objects, and thus you can only interact with them using the methods in the interfaces that we discussed in lecture.

   • Although you aren’t writing this method as part of a class, you should use appropriate Java syntax. The methods should be static and should not return a value.

2. Write a method remAllQueue(Queue<Object> queue, Object item) that takes a queue and an item, and that removes all occurrences of that item from the queue. After the removals, the remaining items should still be in the same order with respect to each other. For example, if you have a queue that contains (from front to rear) {5, 2, 7, 2, 10} and you use the method to remove all occurrences of 2, the resulting queue should contain (from front to rear) {5, 7, 10}. The same guidelines that we specified for remAllStack() also apply here.

• You do not need to submit the Java file, but you should write a program to test your methods before you copy the methods to the part I template. Your submitted methods will be evaluated for correctness.

Problem 5: Using Queues to implement a Stack

10 points; individual-only

In lecture, we considered two implementations of the stack ADT: one using an array and one using a linked list. The following is a third implementation of the stack ADT that uses two queues, Q1 and Q2. The pseudocode belows shows how you could use Q1 and Q2 to implement the stack operations push, pop, and peek.

boolean push( T item ) {

    if (Q1.isEmpty()) {
        Q1.insert(item);
        while (! Q2.isEmpty()) {
            Q1.insert(Q2.remove());
        }
    }
    else {
        Q2.insert(item);
        while (! Q1.isEmpty()) {
            Q2.insert(Q1.remove());
        }
    }

    return true;
}

T pop() {
    if (Q1.isEmpty())
        return Q2.remove();   // will be null if Q2 is also empty
    else
        return Q1.remove();
}

T peek() {

    if (Q1.isEmpty())
        return Q2.peek();   // will be null if Q2 is also empty
    else
        return Q1.peek();
}

Review these algorithms and explain how the two queues, Q1 and Q2 are being used to implement the operations of a Stack. What is the general approach that has been taken? Does this approach make sense? What is the run time efficiency of these methods with? How does it compare to the respective methods in the ArrayStack and LLStack implementations?

Part II

50 points total

Preparing for Part II

Begin by downloading the following zip file: ps8.zip

Unzip this archive, and you should find a folder named ps8, and within it the files you will need for Part II. Make sure that you keep all of the files in the same folder.

Important: When you compile the code in this folder, you may see one or more warnings labeled “unchecked cast”. You can safely ignore them.

Problem 6: Implementing the Bag ADT using a linked list

50 points; pair-optional

This is the only problem of the assignment that you may complete with a partner. See the rules for working with a partner on pair-optional problems for details about how this type of collaboration must be structured.

Earlier in the course, we worked with the ArrayBag class. This class can be seen as an implementation of the Bag abstract data type, which we can specify in Java using the following interface:

public interface Bag {
    boolean add(Object item);
    boolean remove(Object item);
    boolean contains(Object item);
    int numItems();
    Object grab();
    Object[] toArray();
}

In the ps8 folder, we have included:

• the Bag interface (Bag.java)
• a version of the ArrayBag class that includes an implements clause in its header to specify that it implements this interface.

In a file named LLBag.java, write a class called LLBag that implements the Bag interface using a linked list instead of an array. You may use a linked list with or without a dummy head node.

In designing your implementation, you may find it helpful to compare the LLList class, our linked-list implementation of the List ADT, to the ArrayList class, our array-based implementation of that same ADT. In the same way that LLList uses a linked list instead of an array to implement a list, your LLBag class should use a linked list instead of an array to implement a bag.

Notes:

• Make sure that your class explicitly indicates that it implements the Bag interface. To allow your new class to compile, you will need to put it in the ps8 folder with Bag.java.

• Like the LLList class, your LLBag class should use a private inner class called Node for the nodes in the linked list.

• In addition to the methods in the Bag interface, your LLBag class should also have a toString() method that overrides the default toString() method inherited from the Object class. Consult the ArrayBag toString() method to see what the string returned by this method should look like.

• One of the benefits of using a linked list is that there is no need to specify a maximum size—the bag can effectively grow without limit. Therefore, you will not need to provide a constructor that specifies a maximum size, and your add() method can always return true.

• Because the order of the items in a bag doesn’t matter, you can add items to either end of the linked list; however, make sure that your method adds items in O(1) time.

• In general, you should make your methods as efficient as possible. For example, when implementing the remove() method, you should make sure that you don’t traverse the list more than once.

• Copy over the main() method from the ArrayBag class, and make whatever modifications are necessary to allow it to test your LLBag class.

  Important: If you compare the results that you obtain from testing the two classes, you may see that the items are not in the same order in both sets of tests. That is to be expected, and it’s not a problem because items in a bag do not have a position!

Submitting Your Work

• You have read the Java Style Guide (linked on Course page)and followed all guidelines regarding format, layout, spaces, blank lines, and comments;
• ensured that the signature of the methods specified in the assignment have not been changed.
• You have verified that your programs satisfy all the performance tests in the templates;

Submitting your work for Part I

Submit your ps8_partI.pdf file using these steps:

1. If you still need to create a PDF file, open your file on Google Drive, choose File->Download as->PDF document, and save the PDF file on your machine.

2. Click on the name of the assignment in the list of assignments on Gradescope. You should see a pop-up window labeled Submit Assignment. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

3. Choose the Submit PDF option, and then click the Select PDF button and find the PDF file that you created. Then click the Upload PDF button.

4. You should see a question outline along with thumbnails of the pages from your uploaded PDF. For each question in the outline:

   • Click the title of the question.
   • Click the page(s) on which your work for that question can be found.

   As you do so, click on the magnifying glass icon for each page and doublecheck that the pages that you see contain the work that you want us to grade.

5. Once you have assigned pages to all of the questions in the question outline, click the Submit button in the lower-right corner of the window. You should see a box saying that your submission was successful.

Submitting your work for Part II

You should submit only the following files:

• your LLBag.java

Here are the steps:

1. Click on the name of the assignment in the list of assignments. You should see a pop-up window with a box labeled DRAG & DROP. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

2. Add your files to the box labeled DRAG & DROP. You can either drag and drop the files from their folder into the box, or you can click on the box itself and browse for the files.

3. Click the Upload button.

4. You should see a box saying that your submission was successful. Click the (x) button to close that box.

5. The autograder will perform some tests on your files. Once it is done, check the results to ensure that the tests were passed. If one or more of the tests did not pass, the name of that test will be in red, and there should be a message describing the failure. Based on those messages, make any necessary changes. Feel free to ask a staff member for help.

   Note: You will not see a complete Autograder score when you submit. That is because additional tests for at least some of the problems will be run later, after the final deadline for the submission has passed. For such problems, it is important to realize that passing all of the initial tests does not necessarily mean that you will ultimately get full credit on the problem. You should always run your own tests to convince yourself that the logic of your solutions is correct.

6. If needed, use the Resubmit button at the bottom of the page to resubmit your work. Important: Every time that you make a submission, you should submit all of the files for that Gradescope assignment, even if some of them have not changed since your last submission.

7. Near the top of the page, click on the box labeled Code. Then click on the name of each file to view its contents. Check to make sure that the files contain the code that you want us to grade.