Lab 13: Hash Tables; Heap Trees

Task 0: Complete lab evaluations
Task 1: Review hash table basics
Task 2: Practice using a hash table
Task 3: Heap Trees, just the basics

Task 0: Complete lab evaluations

We will begin by taking a few minutes to complete evaluations for the lab component of the course.

These evaluations are only for the teaching fellows/assistants. There is a separate evaluation of the undergraduate course assistants that you will complete, so please don’t comment about the CAs on today’s form.
- A5,B5,C5 Ivan Izhbirdeev
- A4,A6,C4 Patrick Kuzdzal
- B4,B6,C6 Xinyue (Marcia) Ma
- A2,A3,B2 Erin Mcateer
- C3 Justin Sayah
- B3,C2 Conor Walsh
Your evaluations are anonymous, and we will not receive the results until after all final grades have been submitted.
Comments in the text fields are valued and encouraged. Please try to answer all questions, but if a question is not applicable or you do not wish to answer it, you can simply skip it.

Here is the URL that you should use: bu.campuslabs.com/courseeval

Enter your BU login name and Kerberos password, and complete the evaluation for the CS 112 lab section you are registered for. Please do not evaluate your lecture section at this time.
When you are done with the survey, please close the separate browser tab.

Thanks in advance for taking the time to provide your feedback about the labs!

Task 1: Review hash table basics

Your work for this task should be done on paper. Please show your work to a staff member before you leave the lab.

Consider the hash table shown below. Assume that:

It was filled using the hash function from lecture:
```
h(key) = key.charAt(0) - 'a'
```
(In other words, the hash code of a key is the ASCII code of its first character minus the ASCII code of 'a'.)
Collisions were resolved using linear probing.
Gray cells are ones from which an item has been removed.
White cells are ones in which an item has never been inserted.
Occupied cells contain the key of their key-value pair.

0	aardvark
1
2	cat
3	bear
4
5	dog
6

Which item in the table has been inserted incorrectly? How can we be certain?
If we insert an item with a key of "ferret" into the table using linear probing, what is the probe sequence that would be used? (In other words, what sequence of positions would be considered by the insert() method to determine where the item should go?)
If we insert an item with a key of "ferret" into the table using linear probing, where would it end up?

Now consider the following hash table, which was filled using the same hash function but with quadratic probing.

0	aardvark
1	bison
2	cat
3	canary
4
5
6

If we insert an item with a key of "dolphin" into the table using quadratic probing, what is the probe sequence? Where would the item end up?
After inserting "dolphin", we now insert an item with a key of "ant" using quadratic probing. What is the probe sequence? Where would the item end up?
If this table were implemented using the same hash function but with separate chaining, what it would look like? Include both the original keys and the new ones ("dolphin" and "ant").

Task 2: Practice using a hash table

In lecture, we have been considering the OpenHashTable class. Let’s practice writing client code for this class.

Begin by downloading the following zip file: lab13.zip

Unzip this archive, and you should find a folder named lab13, and within it the files you will need for this lab.

Open OpenHashTable.java, write a simple main method to include the following:.

Create an instance of the class:
```
OpenHashTable table = new OpenHashTable(7);
```
This will create an OpenHashTable object with a size of 7. It will use double hashing, because that is the default method of probing in the OpenHashTable class.

Insert several key-value pairs:

table.insert("ant", 23);
table.insert("bee", 10);
table.insert("ant", 30);

If we make the call to insert(), within a System.out.println statement, we will see that this method returns either true (if the key-value pair was successfully inserted) or false (if there was overflow and the key-value pair could not be inserted).
```
System.out.println( table.insert("bee", 50) );
```
Will produce the output:
```
true
```
We can then search for a given key as follows:
```
System.out.prinln( table.search("ant") );
```
Will producce the output:
```
{23, 30}
```
And the statement:
```
System.out.println( table.search("antelope") );
```
Will producce the output:
```
null
```
Note that search() returns either an LLQueue object containing the values associated with the key (which is displayed as a set of values), or null if the key isn’t found.
Now perform the following insertion:
```
table.insert("cow", 10);
```
The key "cow" now has a single value associated with it. Complete the following line of code so that it retrieves the queue containing this value and assigns it to the variable values:
```
Queue<Object> values = _______________________;
```
Check that the queue contains the expected value:
```
System.out.println( values );
```
Will producce the output:
```
{10}
```
Now let’s say that you want to change the value associated with the key "cow" – multiplying its current value (which you should pretend that you don’t know) by 2.

To do so, you will need to do the following:
- remove the current value from the queue, using casting to obtain a value that is an integer:
```
int val = (Integer)values.remove();
```
- insert the doubled value in the queue:
```
values._____________________________
```
  (If necessary, consult the Queue interface to remind yourself of the signature of the method you should use.)
Use the search() method to check that the value associated with "cow" has been changed:
```
_____________________________
```
Will producce the output:
```
{20}
```

Task 3: Heap Trees, just the basics

Your work for this task should be done on paper. Please show your work to a staff member before you leave the lab.

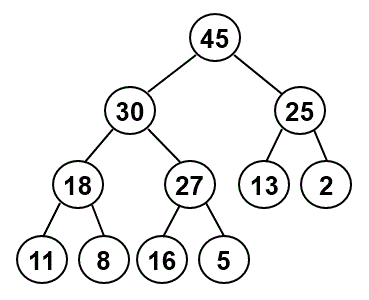
Consider the following heap:

Which node would be in position 4 of the corresponding array?
Given the node in position 4, how could you use arithmetic to determine:
- the position of its left child (if any) in the array
- the position of its right child (if any) in the array
- the position of its parent in the array
If we call the remove() method on this heap:
- Which item will be removed?
- Which item will be copied into the position of the removed item and then be sifted down to restore the heap?
- What will the tree look like after this call to remove()?
What will the heap look like after a second call to remove()? After a third call?
After completing the three calls to remove(), we then use the insert() method to add an item with a key of 21. What will the tree look like after that insertion?