Lecture date: 09/14/99

Prof. John Byers

Scribe: Jisook Youn

Paper: Analysis of the Increase and Decrease Algorithms for Congestion Avoidance in Computer Networks
        -  by Chiu and Jain
 

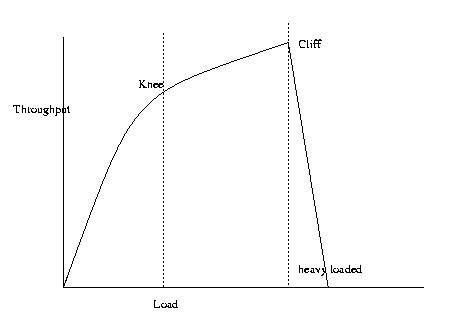
1. Knee is the ideal operating point, because of its short response time and high throughput.
2.  Congestion collapse after the cliff.  Why?
      -  Since packets are staying in the network so long and it may cause the response time
            to be very long, a lot of retransmission may occur.
      -  A lot of packet will be dropped, after using several hops and links. (wasteful)

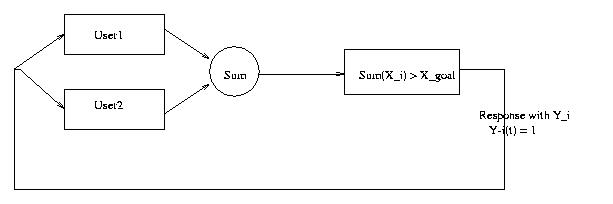
Their assumption on the network model is as the above figure.
       : Synchronous( to simplify their model)
              - flows goes through the network
              - congestion notification bits are set
              - congestion notification bits are received synchronously
       : Distributed
              - all the nodes increase/decrease their load
y(t) = 0 if load may be increased
y(t) = 1 if load has to be decreased
X_i(t+1) = f(Y_i(t), X_i(t))
X_i(t +1) = X_i(t) + (a_i + b_i*X_i(t))
                  =  a_i + (b_i + 1)* X_i(t)
a_i : additive term for this formula
b_i : multiplicative term for this formula

Question 1 from the class: Their assumption about synchronous behavior is problematic.
Comment :  It is very easy to reach unfairness after the knee.
                        By trading fairness, it is easy to get efficiency.

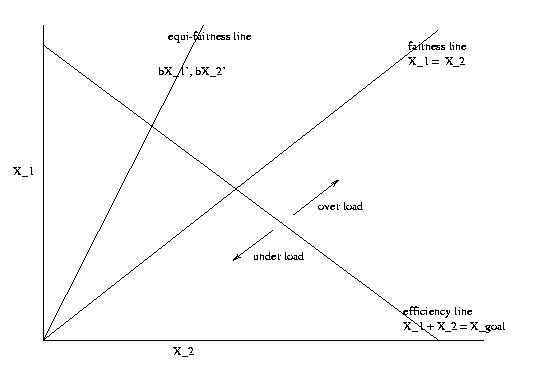
1. All the points on the equi-fairness line has the same fairness.
     ( Fairness index is invariant to multiplicative term.)
2. Fairness metrics(still used in today)
     0 < (Sum(X_i))^2 / n * (Sum(X_i)^2)
     0 implies unfairness, 1 fairness

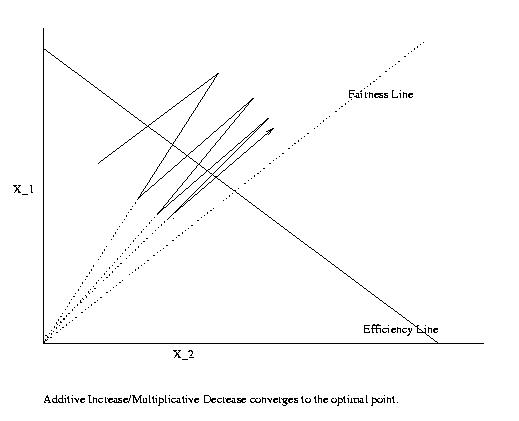
Difference between centralized algorithm and distributed algorithm
When Y(t) = 0 ( Sum(X_i(t ) > X_goal) ) ,
the network will be Sum(X_i(t+1)) > Sum(X_i(t)).
At this situation, the distributed algorithm makes sure that everybody increases the load at time t +1.
However, in the centralized algorithm there is no guarantee that everybody increases its load,  but only
the increase in sum of the total load in the network will be guaranteed.  This can be applied for achieving fairness.

Comments on necessity and sufficiency on their condition.
Given their synchronous and distributed network model assumption, do the conditions they specify
necessarily achieve the theorem?
Does AIMD(Additive Increase Multiplicative Decrease) sufficient to prove the theorem-convergence
to fairness and efficiency?
Actually, they proved this "yes", but they have not proved the necessity of the condition in the paper.
 

Paper : Congestion Avoidance and Control
                - by Van Jacobson

Round-trip-time estimation prior to 1988:
    RTT(t+1) = a * M_new + (a -1) * RTT(t)
    a : low pass filter
a is too large: over bias to recent measurement
a is too small: under bias to variance of measurement
1988: incorporate the variance into RTT_est

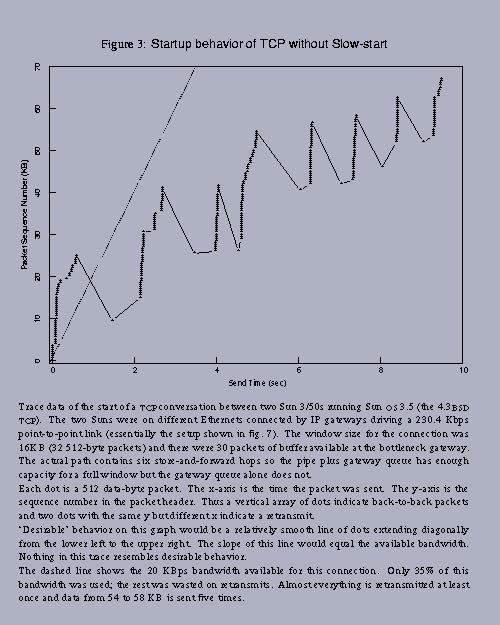
Notice that for example, the packet number 33 is retransmitted about three times, and gets through successfully all three times (!).

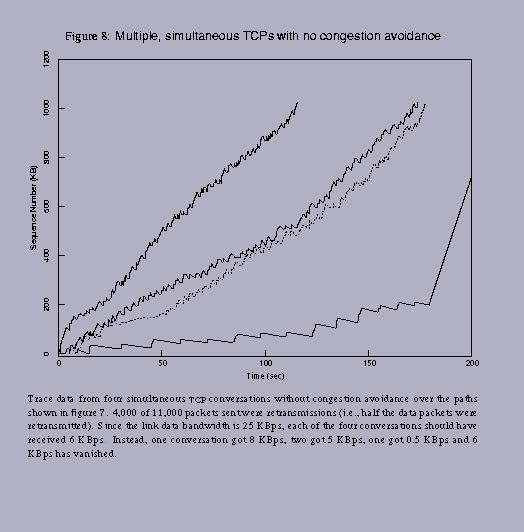
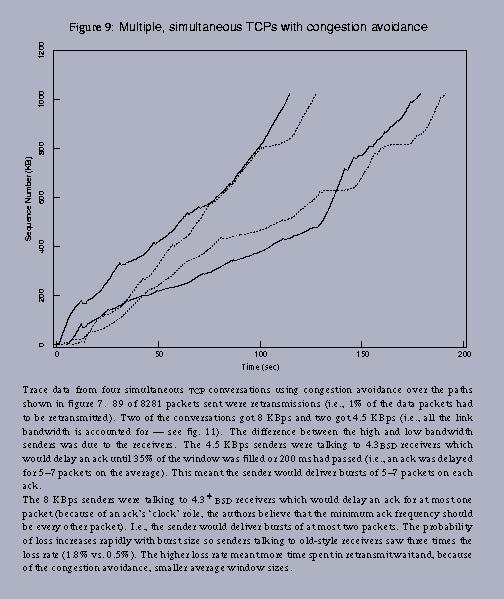
Note that the fairness gets improved in figure 9 from the figure 8.
 

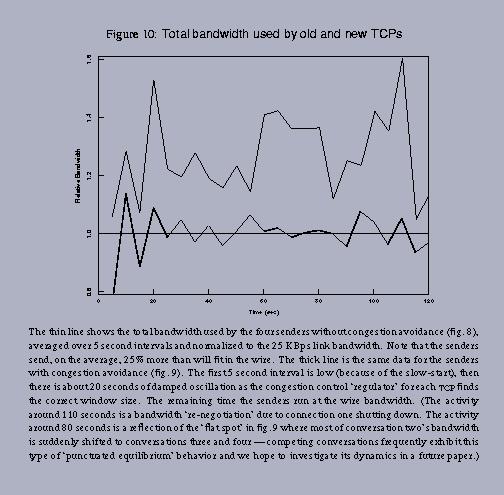
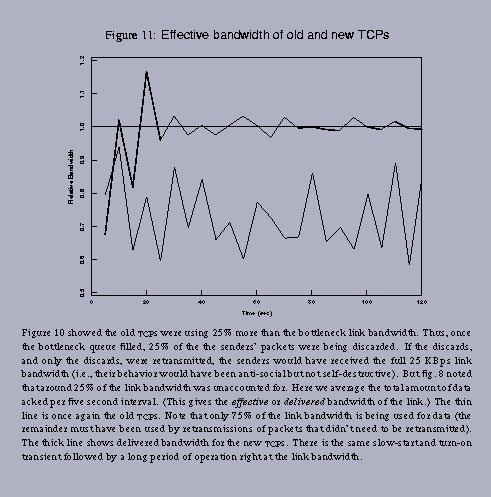
Note that total bandwidth is very high (it actually far exceeds the link capacity!) but effective bandwidth is very low (because the point of operation is beyond the cliff) without congestion control.