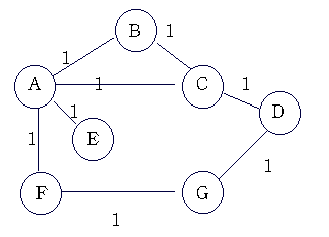
Distance-Vector Routing

: Each node constructs a one-dimensional array containing the "distances"(costs) to all other nodes and distributes that vector to its immediate neighbors.

  1. The starting assumption for distance-vector routing is that each node knows the cost of the link to each of its directly connected neighbors.
  2. A link that is down is assigned an infinite cost.

Example.

 

Information

Stored at Node

 Distance to Reach Node

A

B

C

D

E

F

G

A

0

1

1

¥

1

1

¥

B

1

0

1

¥

¥

¥

¥

C

1

1

0

1

¥

¥

¥

D

¥

¥

1

0

¥

¥

1

E

1

¥

¥

¥

0

¥

¥

F

1

¥

¥

¥

¥

0

1

G

¥

¥

¥

1

¥

1

0

Table 1. Initial distances stored at each node(global view).

 

We can represent each node's knowledge about the distances to all other nodes as a table like the one given in Table 1.

Note that each node only knows the information in one row of the table.

  1. Every node sends a message to its directly connected neighbors containing its personal list of distance. ( for example, A sends its information to its neighbors B,C,E, and F. )
  2. If any of the recipients of the information from A find that A is advertising a path shorter than the one they currently know about, they update their list to give the new path length and note that they should send packets for that destination through A. ( node B learns from A that node E can be reached at a cost of 1; B also knows it can reach A at a cost of 1, so it adds these to get the cost of reaching E by means of A. B records that it can reach E at a cost of 2 by going through A.)
  3. After every node has exchanged a few updates with its directly connected neighbors, all nodes will know the least-cost path to all the other nodes.
  4. In addition to updating their list of distances when they receive updates, the nodes need to keep track of which node told them about the path that they used to calculate the cost, so that they can create their forwarding table. ( for example, B knows that it was A who said " I can reach E in one hop" and so B puts an entry in its table that says " To reach E, use the link to A.)

Information

Stored at Node

Distance to Reach Node

A

B

C

D

E

F

G

A

0

1

1

2

1

1

2

B

1

0

1

2

2

2

3

C

1

1

0

1

2

2

2

D

2

2

1

0

3

2

1

E

1

2

2

3

0

2

3

F

1

2

2

2

2

0

1

G

2

3

2

1

3

1

0

Table 2. final distances stored at each node ( global view).

 

In practice, each node's forwarding table consists of a set of triples of the form:

( Destination, Cost, NextHop).

For example, Table 3 shows the complete routing table maintained at node B for the network in figure1.

Destination

Cost

NextHop

A

1

A

C

1

C

D

2

C

E

2

A

F

2

A

G

3

A

Table 3. Routing table maintained at node B.

 

Link State Routing

: Every node knows how to reach its directly connected neighbors, and if we make sure that the totality of this knowledge is disseminated to every node, then every node will have enough knowledge of the network to determine correct routes to any destination.

Reliable Flooding is the process of making sure that all the nodes participating in the routing protocol get a copy of the link-state information from all the other nodes. As the term " flooding" suggests, the basic idea is for a node to send its link-state information out on all of its directly connected links, with each node that receives this information forwarding it out on all of its link. This process continues until the information has reached all the nodes in the network.

Link State Packet(LSP) contains the following information:

    1. The ID of the node that created the LSP;
    2. A list of directly connected neighbors of that node, with the cost of the link to each one;
    3. A sequence number;
    4. A time to live(TTL) for this packet.

Flooding works in the following way. When a node X receives a copy of an LSP that originated at some other node Y, it checks to see if it has already stored a copy of an LSP from Y. If not, it stores the LSP. If it already has a copy, it compares the sequence numbers; if the new LSP has a larger sequence number, it is assumed to be the more recent, and that LSP is stored, replacing the old one. The new LSP is then forwarded on to all neighbors of X except the neighbor from which the LSP was just received.

Each switch computes its routing table directly from the LSPs it has collected using a realization of Dijkstra's algorithm.

 

Delay Measurement(MRR Page 714)

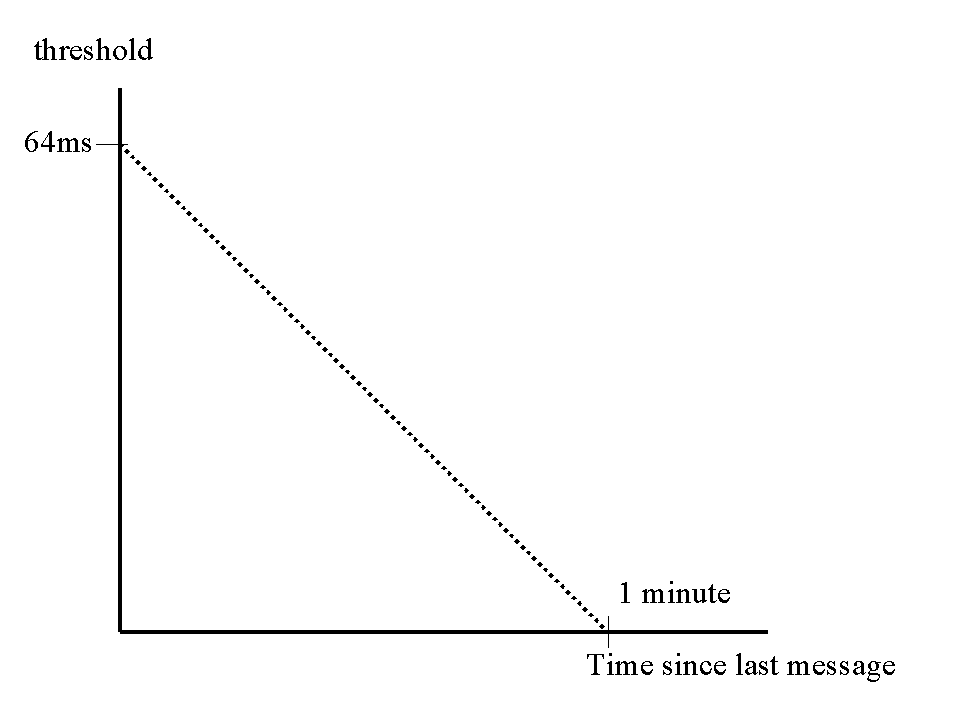
( A longer measurement period = less adaptive routing if conditions actually change.

A shorter measurement period = less optimal routing because of inaccurate measurement.)

When the delay changes by only a small amount, it is not important routing changes. However, whenever a change in delay is long lasting, it is important that it should be reported eventually, even if it is small; otherwise, additive effects can introduce large inaccuracies into routing. A threshold value which is initially high but which decreases to zero over a period time has this effect.

In this paper, the initial threshold is 64 ms. After each measurement period, the newly measured average delay is compared with the previously reported delay. If the difference does not exceed the threshold, the threshold is decreased by 12.8 ms. Whenever a change in average delay equals or exceeds the threshold, an update is generated, and the threshold is reset to 64 ms.

Since the threshold will eventually decay to zero, an update will always be sent after a minute, even if there is no change in delay.

 

The Revised ARPANET Routing Metric

The Revised Link Metric

Normalizing the cost to Hops ( P 49)

Figure 4 illustrates the effect of the transformation for the case of 56 kb/s lines.

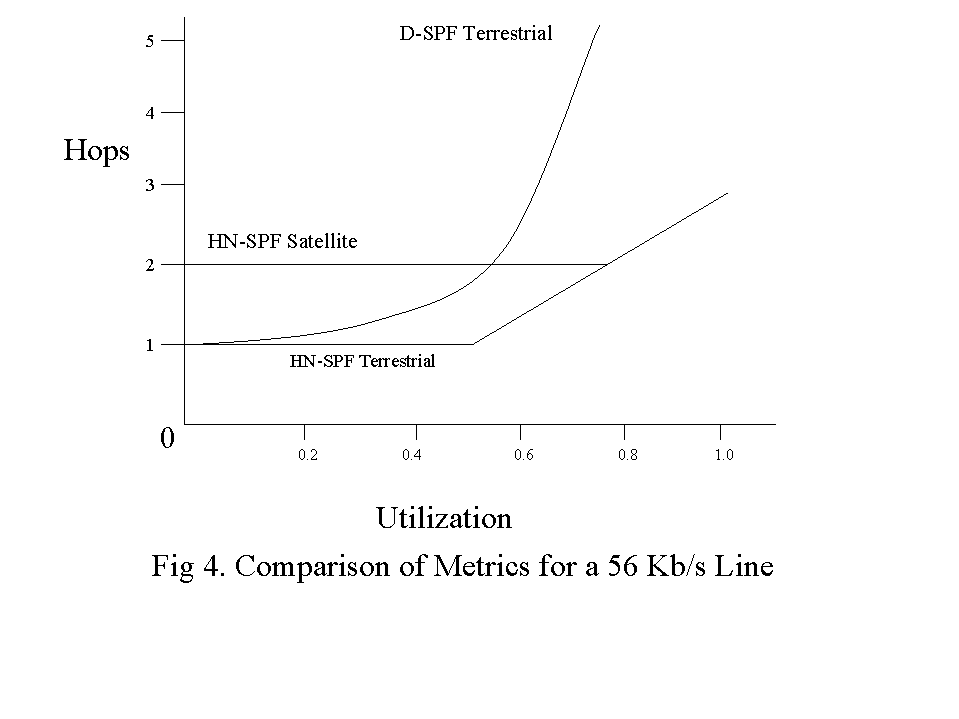
When a link is lightly utilized, there is little reason to shed traffic from the link. The HN-SPF metric is constant until the utilization gets above a threshold that depends on the line-type.

For example, it is 50 % for a 56 kb/s terrestrial link. At higher utilization the cost of the link is allowed to rise in order to shed some of its traffic. The effect of HN-SPF is to make routing reasonably seneitive to the propagation, queueing and transmission delays of links at low utilizations and insensitive to propagation and queueing delays at high utilizations.