Lecture 10/19/99
The paper shows that the packet traffic pattern observed in ethernet is actually self-similar, instead of Poisson. And later different works showed that this same pattern is observed in LAN, WAN and WWW. So this pattern has a very broad scope in computer networks, and it influences the way we model traffic.
To understand the concept of self-similarity, let's consider the process X = {Xt}, in which Xt is a measurement indicating the number of packets transmitted per unit time. Xt can be viewed as a random variable with some known probability distribution function.
Define now new processes Xm as the aggregate of m consecutive measurements:
X tm-m+1 + ... + X tm
Xm t =
------------------
m
Now let's consider what will happen.
In the classical model, packets arrive according to the Poisson model with arrival rate l. The key concept to Poisson arrivals is that they are memoryless, and thus independent of each other. If we aggregate many Independent and Identically Distributed (IID) variables, the probability distribution function of the aggregate converges to a Normal (Gaussian) distribution, and as m increases, the variance of the resulting Normal distribution decreases.
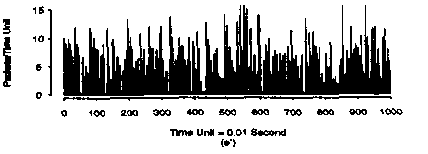
Suppose we performed the following measurements in the time scale specified below. The random variable (y axis) is Poisson distributed and denotes the number of packets per time unit:

We take the samples above and separate them into disjoint groups, with each group formed by 10 consecutive samples. If we computed the mean value for each group and plotted them again, we'd have:
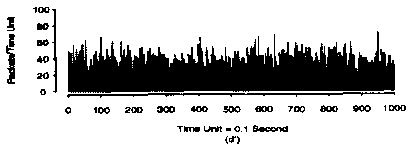
And if we perform the same grouping and averaging operation again, we'd have:
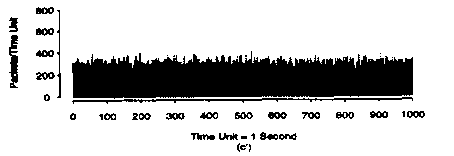
And if we did the same again:
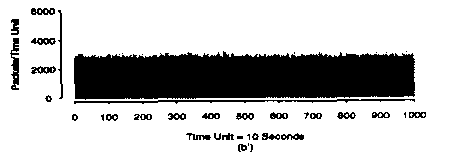
The result is that there is a "smoothing out" of the average number of packets when we increase the time scale.
However, if the process is self similar, then the behavior is different. Consider the original sequence obtained:
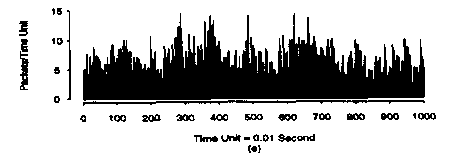
Performing the grouping and averaging operation yields:
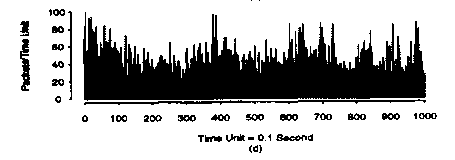
Another operation yields:
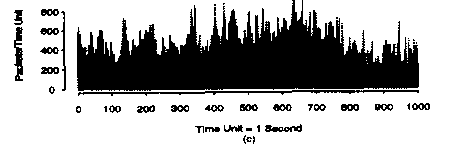
And finally:
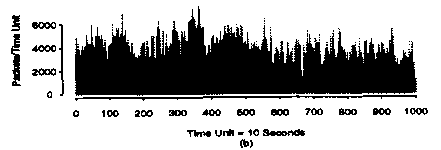
We can see that in this case there is no "smoothing out" of the average value. Clearly, the arrivals of such self-similar process are not independent of one another.
One function that describes the dependence of one variable to the other is the autocorrelation function:
E [ (Xt - u) (Xt+k - u) ]
r(k) = ---------------------
(s)2
Suppose that k = 0, then
E [ (Xt - u) ( Xt - u) ]
E[ (Xt-u)2]
r(0) =
-------------------- = ----------- =
1
(s)2
(s)2
Now suppose that Xt and Xt+k are independent (but they are identically distributed with mean u), then:
E[(Xt-u)(Xt+k - u)]
E[(Xt-u)] E[(Xt+k - u)]
r(k) =
------------------ = -------------------- = 0
(s)2
(s)2
We can see that if arrivals are memoryless (thus subsequent samples are independent but identically distributed), r(0) = 1 and r(k) = 0 for k > 0 . For many physical systems, as k increases to infinity, r(k) goes to 0. And for Self-Similar process, such decay is proportional to:
r(k) | self-similar ~ k -b, 0 < b < 1,
Where b is related to the Hurst parameter H by the following formula:
H = 1 - b/2.
One main consequence of the traffic being self similar is that we will observe large bursts of data even over large time scales. Thus all parts of the network must take that information into account when doing capacity planning, be it at the Web server level, backbone level, etc.
The generation then of self-similar traffic patterns becomes critical
for simulation purposes. It happens that if Xt is the number of packets
per unit time, then if we superimpose many ON-OFF processes Zi(t):
X(t) = Sumi (Zi(t))
X(t) will be a self-similar process if the ON times and the OFF times
are heavy-tailed (for example, drawn from a Pareto distribution).
Because of the self-similar characteristic of the network traffic
and its consequent theoretical long range dependence, there is a need to
study how much it affects the network performance.
The paper presented studied trace data in order to find the relevance of some parameters in terms of loss rate. The parameters considered were H (Hurst parameter), Buffer size (B), Marginal Distribution of the number of packets per unit time, among others.
Some results found in the study are: