The second part of today's class will be on discussing the paper "Architectural Considerations for a New Generation of Protocols" by D. Clark and D. Tennenhouse. This paper actually covers a more general topic than "Beyond Best-Effort Service Models", we will look at some key observations made from this paper regarding the architectural issues of network protocols.
where S_i(tau, t) is the service rate that session i get, and phi_i is the priority assigned to session i. In other words, a busy connection (from now on, we use connection and session interchangably) should get at least a weighted fair share of the total resources (service).
The accumulated traffic generated by connection i, denoted by A_i(0, t), can be depicted by Figure 2 (Figure 4 in P&G paper):
Figure 1: Leaky Bucket
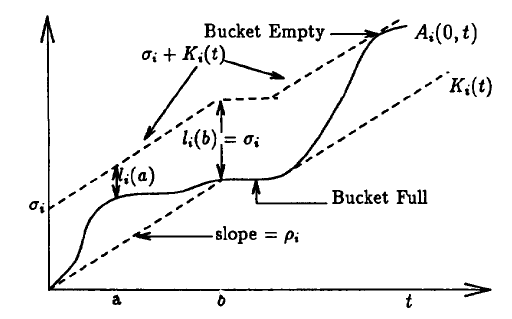
Figure 2: A(t) and l(t)
In other words, A_i(0, t) can be well described (constrained) by the
three parameters given in the Leaky Bucket regulator.
Figure 3: Traffic model
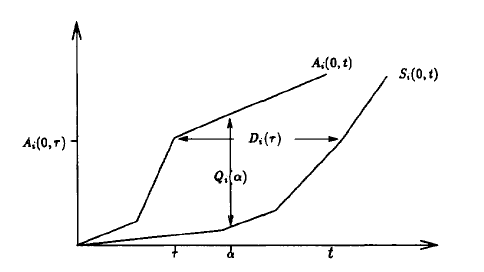
Figure 4: A(0,t), S(0,t), Q(a) and D(a)
In the picture, we use Q_i(a) to denote the queue length for connection i at time a, and we use D_i(a) to denote the delay experience by packet x which arrived at time a. So now the problem becomes: How bad can Q_i and D_i be?
The approach used in the paper can be summarized as follows: First, we simplify the traffic shaper (Leaky Bucket scheme) model by getting rid of the capacity limit C_i, so the source can send a burst of sigma_i packets immediately. And we define a greedy source to be those who send a burst of sigma_i packets at time t = 0, and then keeps sending packets at rate rho_i. It turns out that if all the sources are behaving like this, then we will get the worst case senario in terms of delay and throughput. Formally, we have the following Theorem:
Theorem 1: Let D*_i denote the maximum delay for session
i, Q*_i denote the maximum backlog for session i, i.e.:
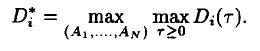and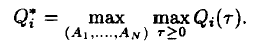 
then both D*_i and Q*_i will be achieved exactly when all sources are
greedy, starting at some fixed time t = 0.
The paper also reveals the following facts:
Fact 1: The system busy period is bounded, where
the busy period is defined as the maximum interval (tau, t) such that: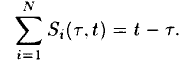 
with normalized service rate.
Fact 2: The connection (session) busy period for
connection i is defined as the time period (tau, t) during which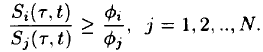 
and the system is busy.
The paper illustrate that when connection is in their busy period, then eventually, the burst injected by this connection will absorbed by other "less busy" connections. Here's an example:
Suppose we have 4 connections, each of them are regulated by a Leaky bucket with steady state rate of 1, and the bursts injected by each source at time t=0 are 3, 1, 0, and 2 respectively. Suppose the totol bandwidth is 5, then at time t=0-, each connection will get a share of 5/4 = 1.25, but since connection 3 don't have burst packet, it doesn't need the extra 0.25 unit of bandwidth, (i.e., connection 3 is "less busy"). Therefore, the leftover bandwidth will be shared by all the other 3 connections, each of which get totally 4/3 unit of bandwidth and the bursts will eventually be absorbed.
The key idea is: even if all sources sent out their maximum burst, it's not enough to prevent the system from entering a steady state in which all sources can get their fair share. This can be depicted by the following Figure (Figure 7 in P&G paper):
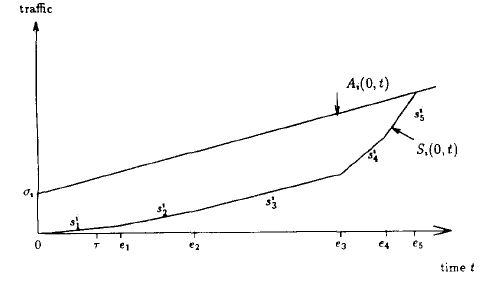
Figure 5: Session i arrivals and departures agter
the begining of a system busy period
The order of the events (depicted by e_j in the figure) depends on the parameters for each connection i: rho_i, phi_i, and sigma_i. Therefore, given these parameters, we can compute Q* and D* for each connection i.
Further discussion: the above analysis can also apply to the overall
system traffic. In other words, we can get the universal service
curve by aggregating the traffic from all N connections, so that
we can get the maximum total queue size and the maximum system delay for
the network. The observation made here is that we need to put an upper
bound on bucket sizes at the ingress points.
Data Manipulation |
Transfer Control |
|
|
|
|
|
|
|
|
|
ADU might consist of several packets data should be passed as soon as possible (even when the dropping probability is high) some packets don't need to be retransmitted.
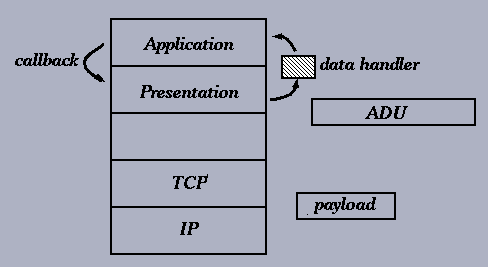
Figure 6: Intergrated Layer Processing
As shown in the figure, ILP tries to "merge" manipulation operations together. For example, since both IP and TCP layer need to perform checksum, why not integrate this operation? In fact, by putting the shared field of TCP packet and IP packet into the shared memory, we can save some operations. Another example is: instead of sending the whole data unit to the Application level, the Presentation level can just send a description of the ADU to Application level, so that the Application level can ignore some useless data by simply respond in its callback function.