These notes are an introduction to the notion of linked lists of nodes in Java. The topics we cover are as follows:
The algorithms are generally presented as Java functions (methods) operating on lists of integers, however, note that the data contained in the nodes could be a generic type.
All the code below assumes the following declaration:
public class Node {
public int item;
public Node next;
Node() { // this would be the default, put here for reference
item = 0;
next = null;
}
Node(int n) {
item = n;
next = null;
}
Node(int n, Node p) {
item = n;
next = p;
}
};
Node head = null; // pointer to the head of a list
These constructors will simplify a number of the algorithms below. For example, to create a list with one element containing the item 5, we could write:
head = new Node();
head.item = 5;
head.next = null; // not actually necessary, since pointers are initialized to null by default
or we can simply use the constructor:
head = new Node(5);
Either will produce:
To add a node containing a 5 to the front of an existing list
we could write
head = new Node(); head.item = 5; head.next = list;
or use the constructor:
head = new Node(5, list);
either of which produces the follow data structure:
We can also "splice" a node into the middle of an existing list, as long as we have a pointer to the node right before the splice; suppose we have a list and a pointer p to a node in the list:
We can add a new node containing 5 after p (i.e., between
the node p and the node p.next) by writing:
Node q = new Node(); q.item = 5; q.next = p.next; p.next = q;
which produces:
Or we can use the constructor:
p.next = new Node(5, p.next);
which produces the same list but without the temporary variable q:
Note that it can also be used to create simple linked lists in a single Java statement. For example, the list just created by splicing could alternately have been created by the following single statement.
Node list = new Node(6, new Node(2, new Node(5, new Node(1))));
In many cases, you have one or more linked lists stored in an ADT object, and you need to manipulate them using ADT methods, and everything is private inside the object. This is the case, for example, in the stack and queue ADT examples of linked lists we studied in lecture. The head pointer, and all the method are private members of the class, for example, here is an object D with an internal linked list and associated methods:
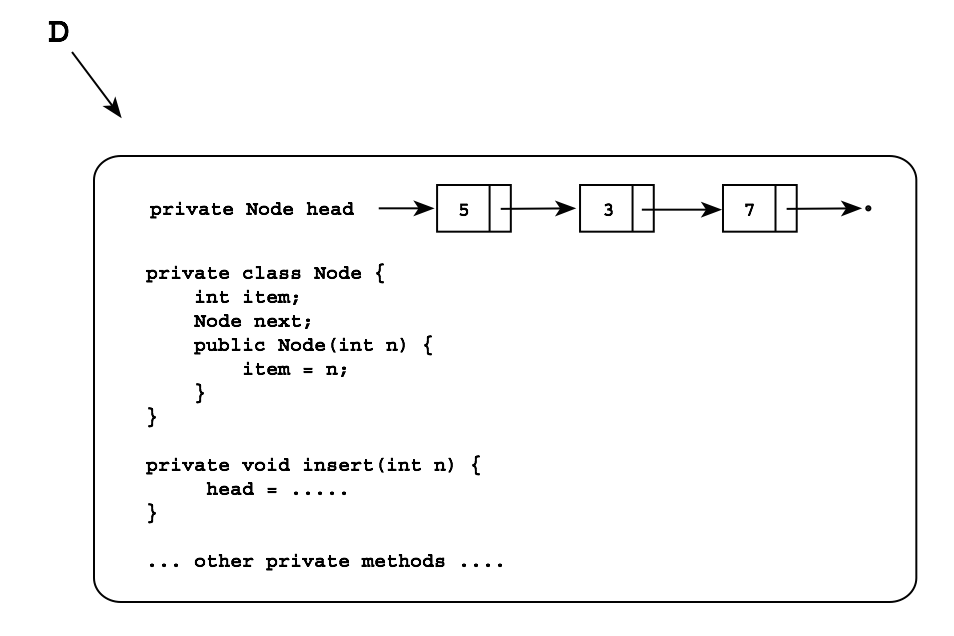
We will assume for the present that we are manipulating a single linked list in this fashion.
The declarations above create an empty list:
Node head = null;
To add to the front of the list, just use the constructor as shown above, changing the pointer head to put a new node between it and the node it points to:
void addToFront(int n) {
head = new Node(n, head);
}
So, here is the result of three calls to addToFront, starting from an empty list:
addToFront(1, head);
addToFront(2, head);
addToFront(6, head);
Do the reverse of the previous method is also a simple example of list manipulation; here we will remove the first element and return the number in the node removed
int removeFront() {
int temp = head.item; // does no error checking for empty lists!
head = head.next;
return temp;
}
You should have recognized the previous two methods as identical to push and pop on a stack!!
The basic thing you do with a list is to "chain along" the list, setting a pointer p to each node in turn and performing
some operation at each node (such as printing out the list). This is done with a simple for loop that initializes
a reference to the first node and stops when it reaches null.
At each iteration of the loop, p will point to each node in the list in turn:
for(Node p = head; p != null; p = p.next ) {
// Do something with each node, such as print out the item
}
OR use a while loop:
Node p = head;
while (p != null) {
// Do something with each node, such as print out the item
p = p.next;
}
This produces the following at each successive iteration of the loop:
At the last iteration, p chains along one more time to point to null, and the
forloop ends:
Note we are guaranteed by the loop condition that p is not null inside the loop, so we can refer to p.item or p.next anytime we want inside the loop without worrying about NullPointerExceptions.
We can then put this code inside a method to do something specific to each member of the list, such as printing it out.
Remember that these methods exist inside an object with a global field head pointing to a linked list.
void printList() {
System.out.print("head -> ");
for(Node p = head; p!=null; p = p.next) {
System.out.print(p.item + " -> ");
}
System.out.println(".");
}
If we want to produce a String representation for the toString() method the ADT, we can do the same thing but collect the results and return them:
public String toString() {
String s = "head -> ";
for(Node p = head; p!=null; p = p.next) {
s += (p.item + " -> ");
}
return s + ".";
}
Another simple example would be finding the length of a list, which can be done by simply keeping a running count inside the for loop:
int length() {
int count = 0;
for(Node p = head; p != null; p = p.next ) {
++count;
}
return count;
}
Exercise A (you may assume the input lists are non-empty):
p.item == k). A simple modification of the previous
technique is to add an if statement to the loop, possibly jumping out of the loop after executing some statements:
for(Node p = head; p != null; p = p.next )
if( B ) {
// do something to the node that p refers to
break; // if you want to stop the chaining along
}
Note, again, that we can refer to p.item and p.next in the loop body with no worry of a NullPointerException, because we have already checked that p != null in the for loop condition. A more compact way of writing this loop is to put the negation of the if-statement condition into the for loop condition:
for(Node p = head; p != null && !B; p = p.next ) {
// etc.
}
For example, if we wish to set the pointer q to point to the first negative number in the list (or null if no such number exists) we could write the following:
Node q = null;
for(Node p = head; p != null && p.item >= 0; p = p.next ) {
q = p;
}
// now q points to first negative number or null if not found
Note that we have to move the delaration of the loop variabe outside the loop if we wish to refer to it after the loop; so we could the same as the previous more compactly as follows:
Node q = null;
for( ; q != null && q.item >= 0; q = q.next ) {
;
}
// now q points to first negative number or null if not found
OR, use a while loop:
Node q = null;
while (q != null && q.item >= 0) {
q = q.next;
}
Exercise B
Chaining down a list is often combined with some kind of modification of the structure of the list, for example, you might want to insert or delete a node. We will consider node deletion as an example to illustrate the basic problem with a singly-linked list: a list goes in one direction, and you can't go backwards!
Suppose you want to delete the node pointed to by p in the following list:
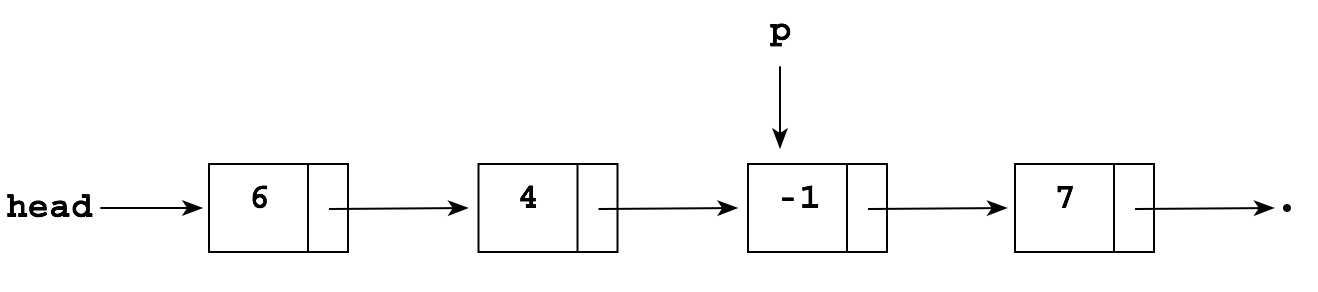
The problem is that to delete the -1, you need to "reroute" the pointer in the node containing 4 "around" the -1 so that it points to the node containing 7:
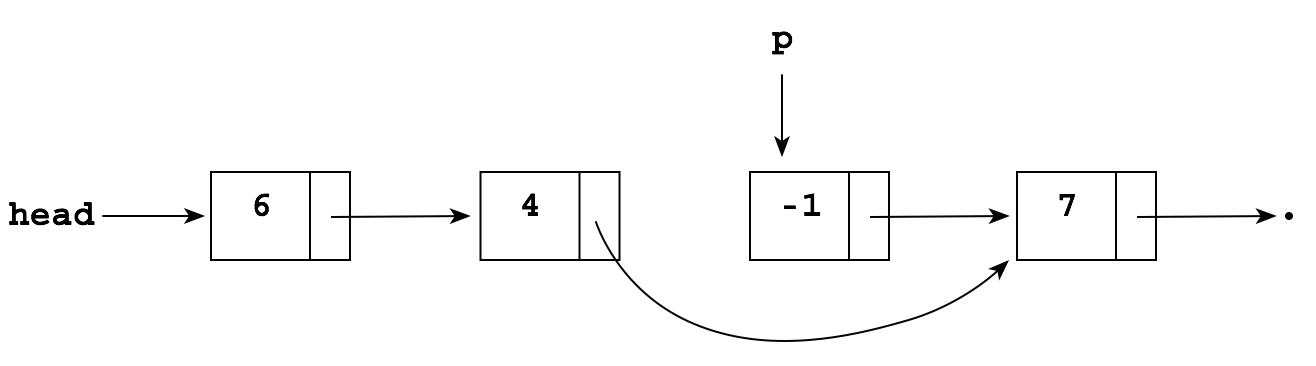
But you don't have a pointer to the node containing 4! The simplest solution is just to keep a "trailing pointer" q that follows p as it chains along, always pointing to the node before p:
Now, to delete the -1, we can simply perform the following to "reroute" the next pointer in q to point to the node after p: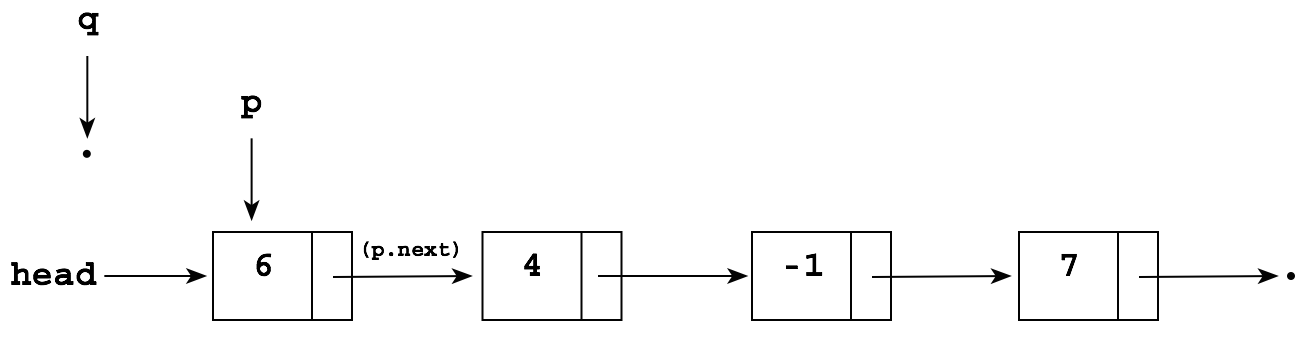
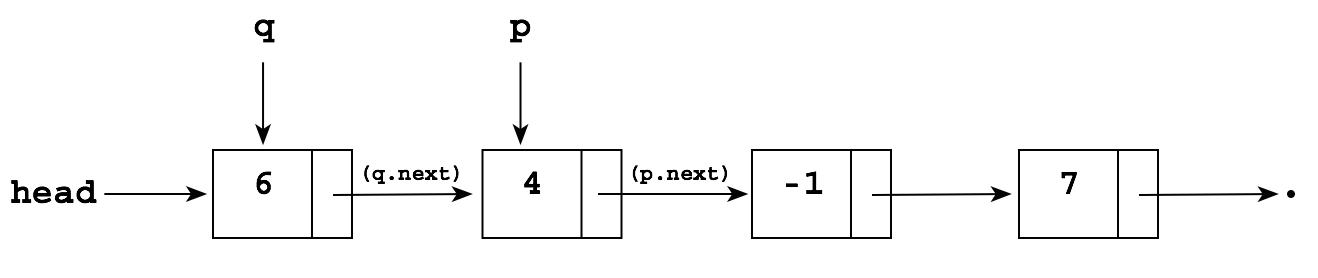

q.next = p.next;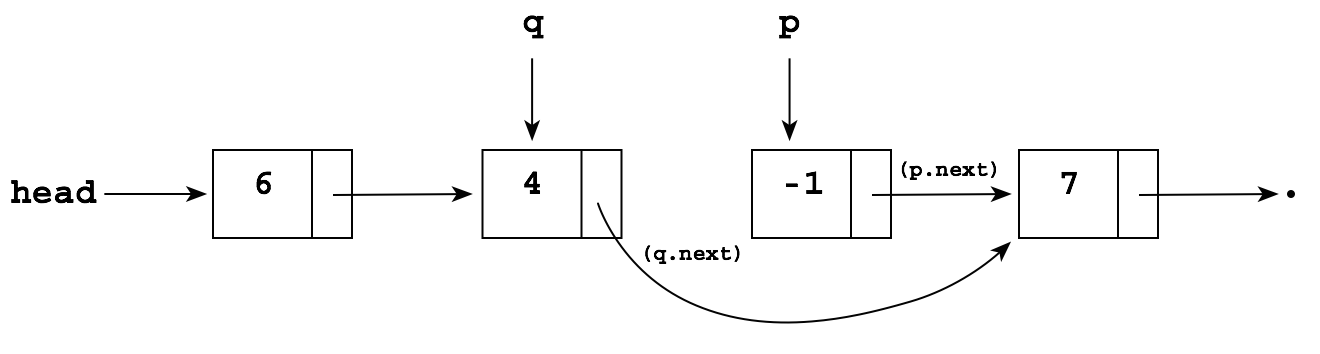
This general technique is sometimes called the "inchworm" since the movement of the two pointers is like the way an inchworm moves its body.
Node p = head;
Node q = null;
while( p != null ) { // During first iteration, p points to first element and q has no value;
// thereafter, p points to a node and q points to the previous node
q = p;
p = p.next;
}
// OR, using a for loop:
for(Node p = head, Node q = null; p != null; q = p, p = p.next ) {
// During first iteration, p points to first element and q has no value;
// thereafter, p points to a node and q points to the previous node
}
But it is a little bit complicated! What if we want to delete the first node? What if the list is empty? These are the special cases that make iterative algorithms a bit messy (we'll introduce a technique to avoid some special cases in the next section).
For example, to delete the first node in the list containing a negative number, we could do the following:
void deleteNegative() {
if( head == null) // Case 1: List is empty, do nothing
;
else if( head.item < 0 ) // Case 2: have to delete first node?
head = head.next; // Yes, so reroute around the first node
else { // Case 3: Don't have to delete first node, so can use inchworm
Node p = head.next; // p points to second node
Node q = head; // q points to first node
while( p != null ) {
if( p.item < 0 ) {
q.next = p.next;
break;
}
q = p; // chain along, and keep q trailing p
p = p.next;
}
}
}
// OR, using a for loop:
void deleteNegative() {
if( head == null) // Case 1: List is empty, do nothing
;
else if( head.item < 0 ) // Case 2: have to delete first node?
head = head.next; // Yes, so reroute around the first node
else { // Case 3: Don't have to delete first node, so can use inchworm
for(Node p = head, Node q = null; p != null; q = p, p = p.next ) {
if( p.item < 0 ) {
q.next = p.next;
break;
}
}
}
}
In general, the Inchworm technique is the easiest way to manage this problem, so we will use it in the rest of these notes. However, be careful about those special cases! In general, we have to worry about the following cases when modifying a linked list:
Although in a simple linked list, you need to go through the entire sequence to get to the last node, when you need to routinely access the end of the list (e.g., successively adding to the end of the list), it is useful to maintain a pointer to the last node.
Here is a simple method which uses a global definition of a pointer to the last node:
Node head = null;
Node last = null;
void addToEnd(int n) {
if(head == null) { // if head is null, then must initialize last pointer
head = new Node(n,null);
last = head;
}
else {
last.next = new Node(n,null);
last = last.next; // chain along to update last pointer to new last node
}
}
You may have noticed that you have seen this algorithm before: addToEnd is the same as enqueue(...) for a queue....
The deleteNegative example showed that it is often messy to deal with the special cases involving a global head pointer. Even worse, we have to have access to the exact head variable inside the method, so you would have to write a method like this for each list (i.e., you can't just write one method to be used on all such lists).
The simple solution to this is of course to parameterize the head pointer in the methods. The head pointer is made a parameter to the method, and the (possibly) new head pointer is returned as the result of the method. A few examples will clarify this important technique, which we will make extensive use of.
Supposing that we do not need to make any changes to the list, then we simply rewrite our methods to take the head pointer as a parameter:
int length(Node h) {
int len = 0;
for(Node p = h; p != null; p = p.next ) {
++len;
}
return len;
}
// To use:
int len = length(head);
Compare this with the version first presented above!
If we need to modify the head pointer, then we return the necessary value through the method. Here is a new version of addToFront using this technique:
Node addToFront(int n, Node h) { return new Node(n, h); } // How to use it: head = addToFront(1, head);
Often this technique will remove some messy special cases. For example, the previous algorithm to delete the first negative number in a list could now we written as:
Node deleteNegative(Node h) {
if(h == null) { // only special case now
return null;
}
else {
Node p = h.next; // p points to second node
Node q = h; // q points to first node
while( p != null ) {
if( p.item < 0 ) {
q.next = p.next;
break;
}
q = p; // chain along, and keep q trailing p
p = p.next;
}
}
}
// to use it:
head = deleteFirstNegative(head);
This technique can still be used when the head pointer is a global field in the ADT. We will make consistent use of this idiom in the "cookbook" of iterative algorithms below, and also in our recursive algorithms. It is a powerful technique and you should try to use it whenever possible.
Exercise C
void printList() {
System.out.print("head -> ");
for(Node p = head; p!=null; p = p.next) {
System.out.print(p.item + " -> ");
}
System.out.println(".");
}
You would call the method like this:
printList(head);
int length(Node h) {
int count = 0;
for(Node p = h ; p!=null; p = p.next)
++count;
return count;
}
This next function is a standard one; it returns a true or false depending on whether the number is in the list:
boolean member(int n,Node h) {
for(Node p = h; p != null; p = p.next )
if( p.item == n )
return true;
return false; // return null if item not found
}
This is a variation of the previous: it returns a pointer to the node containing a number, or null if it is not in the list:
Node find(int n,Node h) {
for(Node p = h; p != null; p = p.next )
if( p.item == n )
return p;
return null; // return null if item not found
}
Here is a version of delete which removes the first instance only of a specific number from the list; as observed above, the complication is that we have a number of special cases, depending on where the node to be deleted is.
Node delete(int n, Node h) {
if(h == null) // case 1: list is empty, do nothing
return null;
else if(h.item == n)
return h.next; // case 2: item to delete is the first node
else { // case 3: find the node before n using the inchworm technique
for(Node p = h.next, q = h; p != null ; q = p, p = p.next ) {
if( p.item == n ) {
q.next = p.next;
return h; // return original head pointer, since it does not change
}
}
}
}
// You would call the method like this:
head = delete(23,head);
We have shown above how easy it is to insert
an item into the first position using the Node() constructor; inserting into
a sorted list (in ascending order) is quite similar to the delete algorithm and again uses the
two-pointer technique. In this algorithm we will use a while loop just to show how that works, as compared with the for loop.
Node insertInOrder(int n, Node h) {
if(h == null) // case 1: list is empty -- add to front and return pointer to new first node
return new Node(n,h);
else if(h.item >= n) // case 2: n should be before the first node -- again add to front
return new Node(n, h);
else { // case 3: find the node before where n should be using the inchworm technique
Node p = h.next;
Node q = h;
while( p != null ) {
if(p.item >= n) { // found insertion point, between p and q
q.next = new Node(n, p);
return h; // since first node did not change, return original head pointer
}
q = p; // chain along!
p = p.next;
}
q.next = new Node(n, null); // case 4: Node must be added at end of list
}
}
// You would call this as follows:
head = insertInOrder(23,head);
The technique here is to simply chain down a list, making a copy of each node, and adding to the end of a new list:
Node copyList(Node h) {
Node p = h;
if(p == null) // Case 1: list is empty
return null;
else { // Case 2: list has at least one node
Node q = new Node(p.item); // put first node in place in copy
Node last = q; // Maintain a pointer to the last node to facilitate adding to the end of the list
p = p.next;
while( p != null ) {
last.next = new Node(p.item);
last = last.next; // chain along original list and with the last node in new list
p = p.next;
}
return q;
}
}
// You would call this as follows:
Node copyHead = copyList(head);
This algorithm is probably one of the most difficult for linked lists; it uses three references which chain down the list together and rearrange the pointers so that node q, instead of pointing to p, now points to r; doing this for each node reverses the entire list. This was a standard exam question on the PhD Qualifying Exam at UPenn when I was a student there..... I've also heard that it is a common interview question at software companies!
Node reverse(Node h) {
if(h == null)
return null;
Node p = h.next, q = h, r;
while ( p != null ) {
r = q; // r follows q
q = p; // q follows p
p = p.next; // p moves to next node
q.next = r; // link q to preceding node
}
h.next = null;
return q;
}
// to use:
head = reverse(head);
Here is another solution to the previous problem, but creating a new list is much easier: we think of the new list as a stack, and just push new nodes on it as we go down the input list:
Node reverse2(Node h) {
if(h == null)
return null;
Node q = null
for(int p = h; p != null; p = p.next) {
q = new Node(p.item, q);
}
return q;
}
Exercise E
arrayToLinkedList(...) which takes an array of integers and creates a linked list with the same elements in the same order;equalLists(...) which takes two lists and determines if they are identical (have the same elements in the same order);
The special cases 1 and 2 in these algorithms, when you need to worry about whether you need to change the head pointer, causes significant problems:
You have to write these special cases into the algorithms, as we have seen above; and
You must write a separate method for EACH linked list, as the pointer head must be explicitly mentioned in the algorithm.
This latter problem is really the most important, as it makes us write multiple versions of the same code, which, as we saw in the case of generics, is a real problem. We would like to write ONE method which can be used for all such lists. This will be solved elegantly when we use recursion, but we can solve the problem in the iterative case by using a dummy first node that contains no value (or a sentinel value, such as Integer.MIN_VALUE) as a item. In this case, you would initialize your list using:
Node head = new Node();
Alternatively, and sometimes very usefully, we can use the header node to store useful information such as the length of the list. The general outline of a for loop which chains down a list keeping a training pointer is now as follows. (We will show the differences from the previous methods in red -- you will see the the differences are usually quite minimal!)
for(Node p = head.next, q = head; p != null; q = p, p = p.next ) {
// During first iteration, p points to first element and q to the header node;
// thereafter, p points to a node and q points to the previous node
}
For example, if we want to eliminate the first node in our list which contains a negative number, we would write the following:
for(Node p = head.next, q = head; p != null; q = p, p = p.next ) {
if( p.item < 0 ) {
q.next = p.next;
break;
}
You do not HAVE to use such a dummy header node, especially if you are not modifying the lists; when you are inserting or deleting nodes, however, they make your life simpler. In any case, they are unnecessary for recursive algorithms, as we shall see.
void printList() {
for(Node p = head.next ; p != null; p = p.next )
System.out.println(p.item);
}
You would call the method like this:
printList();
int length() {
int count = 0;
for(Node p = head.next ; p!=null; p = p.next) {
++count;
}
return count;
}
You would call the method like this:
int n = length();
Node lookup(int n) {
for(Node p = head.next; p != null; p = p.next )
if( p.item == n )
return p;
return null; // return null if item not found
}
You would call the method like this:
Node q = lookup(34);
void delete(int n ) {
for(Node p = head.next, q = head; p != null ; q = p, p = p.next )
if( p.item == n ) {
q.next = p.next;
return; // if you delete this line it will remove all instances of the number
}
}
You would call the method like this:
delete(head,23);
void insertInOrder( int n ) {
Node p = head.next; // p points to first real node in list
Node q = head; // q trails p
while( p != null ) {
if(p.item >= n) { // found insertion point, between p and q -- This is case 3
q.next = new Node(n, p);
return;
}
q = p;
p = p.next;
}
q.next = new Node(n, null); // Node must be added at end of list --- This is case 4
}
You would call the method like this:
insertInOrder(23);
void reverse() {
if(head.next == null) // empty list
return;
Node p = head.next, q = head, r;
while ( p != null ) {
r = q; // r follows q
q = p; // q follows p
p = p.next; // p moves to next node
q.next = r; // link q to preceding node
}
head.next.next = null;
head.next = q;
}
reverse(head);