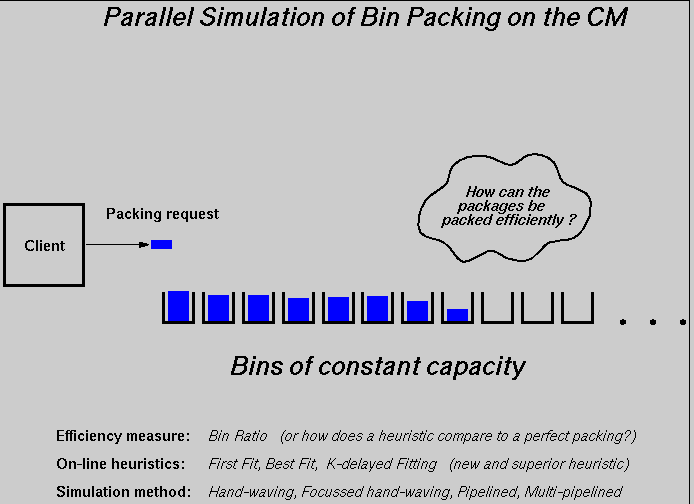

Bin packing is the study of packing a series of requests (or weights) into a number of fixed size resources (or bins). This series of requests usually follows a specific distribution. For a given number of such requests, Optimal fit is the arrangement of values that uses the fewest number of bins. Finding this ``Optimal arrangement'' is known to be exponentially difficult. Therefore online heuristics to approximate this optimal performance have been suggested (An online heuristic must sequentially service the requests as they arrive with no reordering of weights in the bins). One such heuristic is the well-known First Fit approximation where the bins are inspected sequentially and the newly arriving weight is placed in the first bin that has enough room for it. Another heuristic for approximating optimal fit is Best fit. In Best Fit, the new weight is placed in the bin that will leave the smallest possible unfilled space. For many practical distributions the performance of these heuristics is acceptable and quite close to optimal. However, an interesting question is how well do these heuristics approximate optimal fitting. The aim of this laboratory project is to use the CM-5 to study the asymptotic behavior of these heuristics when the number of requests to be serviced approaches infinity.
Simulation Model
We htmlassume that the requests (weights) to be packed follow a uniform distribution over the interval (a,b) , for 0 <= a <= b < 1. To judge the goodness of a given packing (how dense the packing is), we define the Bin Ratio to be the ratio between the total available space and the total used space of all bins in use. Obviously, we would like this ratio to approach unity, in which case we have a Perfect Packing. Without loss of generality, we assume each of the bins has a unit size. Therefore, for a packing that uses n nonempty bins 1, 2, 3, ... , n, where the available space in bin i is h(i), the bin ratio is given by the formula:
BR = n / [ n - ( h(1) + h(2) + ... + h(i) + ... + h(n) ) ]An interesting question is the characterization (via simulation) of First Fit (or any other heuristic) for arbitrary values of a and b . A straightforward serial simulation for the First Fit heuristic would require an O(n^2) steps, where an O(n) number of steps is needed to service (pack) a new request. The purpose of this lab is to investigate potential speedups using parallel simulation algorithms.
The inherently sequential nature of the bin packing simulation is evident from the observation that: ``To take any actions or decisions on behalf of a request, all the previous requests should have been processed''. That is, we cannot decide where a weight should go unless all the preceeding weights have been already packed. In other words, we cannot aim at processing requests concurrently and thus, no control parallelism can be exploited in this problem. Since at least one step would be required to be able to service a request, and the steps for the $n$ requests are necessarily sequential, it follows that a lower bound on any deterministic algorithm for bin packing is O(n) . The question is whether this lower bound can be achieved. If this is possible then it follows that the amount of processing per request should be constant (independent of the size of the problem).
The Exercise:
Sample Results:
Date of last update: May 22, 1994.