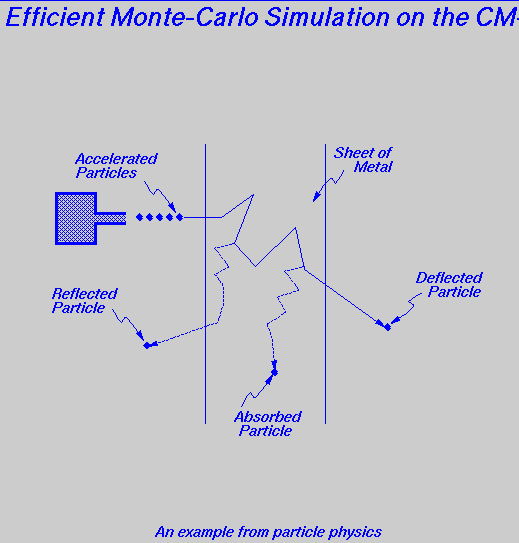
CS-551: Homework/Lab Assignment -- Neutron Scattering Simulation

Problem Description:

The Connection Machine is to be used to perform a simulation to estimate the probability that an accelerated particle aimed at a thin sheet of metal will be reflected, deflected, or absorbed. The experiment works as follows:

Initially, the particle is aimed at an angle perpendicular to the sheet.
Each step of the simulation concerns itself with the journey of the particle as it bounces from one atom to another.
At any given iteration, the distance traveled, which follows an exponential distribution, can be calculated using the equation:
```
  d = L * ln( 1 / [1-rnd()] ) 
```
where, rnd() is a uniformly-distributed random value and L is a constant that depends on the metal under test (L is the average distance traveled in one iteration).
As a result of hitting an atom at the end of a given iteration, the particle's trajectory direction is changed by an angle r. The rotation angle in radians is a random variable that can be generated using the equation:
```
 r = 2 * pi * (1/K) * (r1 + r2 + r3 + ... + ri + ... + rK) - pi 
```
where, ri , 1 <= i <= K are uniformly distributed random variables and K is a constant that depends on the metal under test.
After each iteration, if the perpendicular distance traveled by the particle through the metal exceeds the thickness T of the sheet then the particle is considered to have been deflected. If the perpendicular distance traveled is negative then the particle is considered to have been reflected. The particle is considerd to have been absorbed if the total distance traveled (in any direction) is greater than M * L, for some large value M .

The Exercise:

Write a SIMD-style C* program to simulate the described experiment on the CM-5. Your program should maximize the utilization of the connection machine.

Remarks:

Your program should use the CMSSL library to generate a set of "parallel" random numbers. In particular, the CMSSL_fast_rng function uses a lagged-Fibonacci algorithm to generate pseudo-random numbers and stores them in a parallel variable.
In order to compare the efficiency of your implementations, you may want to use the CM timers SIMD timing facility on the CM-5.
For debugging and demonstration purposes, your program should be able to maintain a distribution of the particles in their journey through the sheet. This could be done by maintaining a 2D-shaped integer that represents the number of particles in the plane parallel to the original trajectory of the particles.

Hints:

This document has been prepared by Professor Azer Bestavros <best@cs.bu.edu> as the WWW Home Page for CS-551, which is part of the NSF-funded undergraduate curriculum on parallel computing at BU.

Date of last update: October 3, 1994.