The Scaling Estimator
Mark E. Crovella and Murad S. Taqqu
A Tool For Estimating the Heavy Tail Index from Scaling Properties
The software available from this page provides an estimation of the tail
index alpha for empirical heavy-tailed distributions, such as have been
encountered in telecommunication systems. It uses a method (called the
``scaling estimator'') based on the scaling properties of sums of
heavy-tailed random variables. It has the advantages of being
nonparametric, of being easy to apply, of yielding a single value, and
of being relatively accurate on synthetic datasets. Since the method
relies on the scaling of sums, it measures a property that is often one
of the most important effects of heavy-tailed behavior. Most
importantly, the scaling estimator increases in accuracy as the size of
the dataset grows, meaning that it is particularly suited for large
datasets, as are increasingly encountered in measurements of
telecommunications and computing systems.
This software ("aest") is written in C for Unix operating systems. To date it has
been tested on SGI systems running IRIX 5.3 and Sun systems running SunOS 5.4.
To retrieve the software, click on the link below, save the result to a file (say aest.tar)
type "tar xvf aest.tar", then type "make".
In addition to providing an estimate of the tail index, aest can provide
graphical output that can help interpret its results.
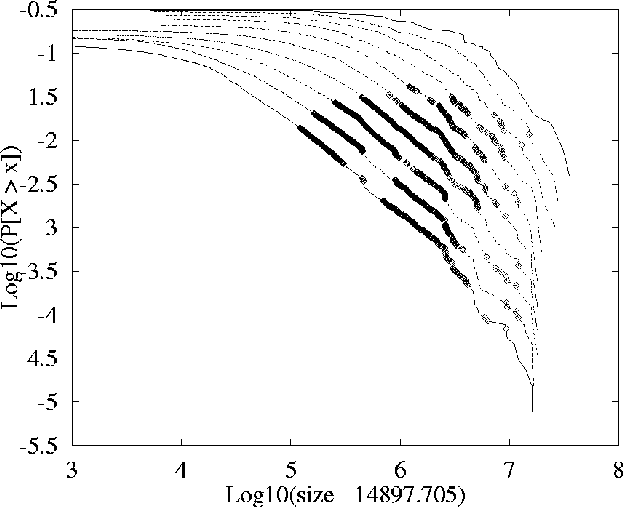
This figure shows an example of the graphical output from aest
(Figure 12 from the paper below). The dataset
used is a set of files stored on Web servers and the figure shows the LLCD
plots of successive aggregations of the dataset, along with the portion of
the tail judged by aest to be the region over which power-law scaling is taking
place.