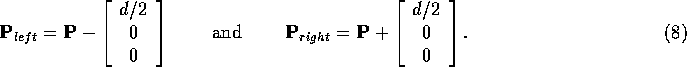.
There will be no scaling in the directions perpendicular to the
scaling axis. If the vector U were the x axis, then the scaling
matrix would simply be:
Therefore, our strategy will be to find the rotation matrix that takes the
axis into the x axis. We do this by defining an object coordinate
system with 
as the x axis.
To obtain such a coordinate system, we need define the two other axes,
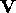and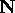 
. Since there is no scaling along the other
two axes, we can choose any unit vectors 
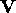and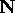 
as
long as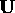 
, 
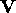and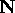 
are orthogonal. There are
many vectors that satisfy these conditions. For example, we can
construct a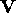 
axis perpendicular to 
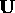as follows:
assuming that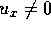 
or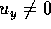 
.
The third axis can be found via a cross product:
We now have an object coordinate frame defined by unit vectors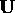 
,
,
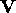and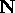 
. To rotate from the object coordinate frame into the world
coordinate frame, we use the rotation matrix:
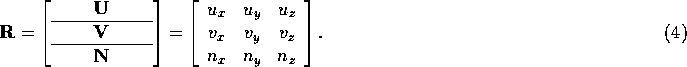
Finally, the matrix for scaling along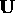 
can be written:
where we first rotate from object coordinates into world coordinates, then scale along x, and then rotate back.
in
the diagram below. This is a side view (looking at the x-z
plane), showing projection with PRP at the origin, and the viewplane
perpendicular to the z axis.
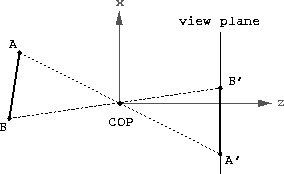
By tracing rays from the points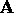 
and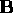 
through the
center of projection (COP), we can determine their projections on the
view plane. The rays are shown as dashed lines, and the segment's
projected end points are shown as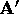 
and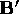 
in the
figure. From this picture we can see how objects behind the COP will
be projected upside-down and flipped.
This is also demonstrated by looking at the math. Projection of the
end point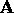 
in front of the center of projection can be
written:
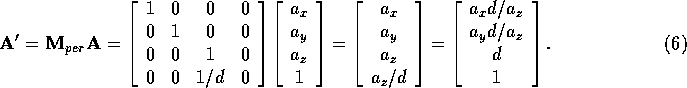
If we move the end point behind the center of projection by negating it's z component, then we get:
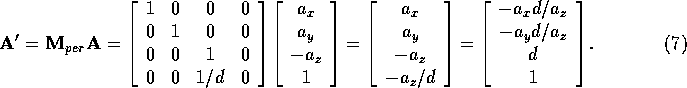
We can see that the sign of the of the projected point's x and y coordinate are flipped.
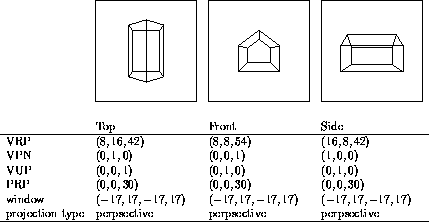
The resulting projections are shown along the top row of the table. Note that the projection reference point (PRP) is the same for each view. The PRP can be the same for each view because the point is expressed in view reference coordinates, and therefore it moves with the camera.
, the point between
the eyes is given in view reference coordinates.
The diagram below depicts the position of the eye points for
the stereo views.
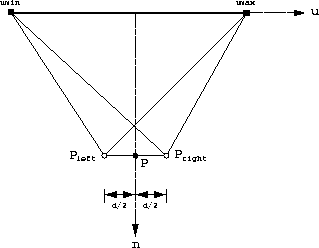
The left eye point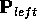 
is displaced by 
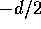along the
u axis, and the right eye point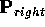 
is displaced by
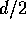along the u axis. This can be written in vector form:
