Color-based Skin Tracking Under Varying Illumination:
Experiments

 IVC Logo
Fig. 1: Examples frames from sequences used for experimentation.

Experimental Data Set with Labeled Ground Truth

To evaluate the performance of our system we collected a set of 21 video sequences from nine popular DVD movies. The sequences were chosen to span a wide range of environmental conditions. People of different ethnicity and various skin tones are represented. Some scenes contain multiple people and/or multiple visible body parts. Collected sequences contain scenes shot both indoors and outdoors, with static and moving camera. The lighting varies from natural light to directional stage lighting. Some sequences contain shadows and minor occlusions. Collected sequences vary in length from 50 to 350 frames; most, however, are in the 70 to 100 frame range.

All experimental sequences were hand-labeled to provide the ground truth data for algorithm performance verification. Every fifth frame of the sequences was labeled. For each labeled frame, the human operator created one binary image mask for skin regions and one for non-skin regions (background). Boundaries between skin regions and background, as well as regions that had no clearly distinguishable membership in either class were not included in the masks and are considered {\em don't care} regions. The segmentation of these regions was not counted during the experimentation or evaluation of the system. The figure below shows one example frame and its ground-truth labeling.

(a) (b)
(c) (d)
Fig. 2: Example of a labeled ground truth frame: (a) original image from a sequence in which a hand is shown reaching to lift a drinking glass, (b) corresponding labeled ground truth mask image for skin, (c) background, and (d) don't care regions. Boundaries between skin regions and background, as well as regions that had no clearly distinguishable membership in either class were not included in the masks and are considered don't care regions.

Performance Experiments

The performance of the system was evaluated using the determinant of the confusion matrix criterion. The determinant of the confusion matrix was computed for every hand-labeled frame of the sequence. To gain an aggregate performance metric for the sequence, the average determinant of the confusion matrix was computed.

For comparison, we measured the classification performance of a standard static histogram segmentation approach on the same data set. The static histogram approach implemented used the same prior histograms and threshold as our adaptive system (see the technical report for more details). The same binary image processing operations of connected component analysis, size filtering, and hole filtering were performed to achieve a fair comparison.

  Classification Performance
Sequence Info Static Dynamic
# \char93 frames skin bg Det[C] skin bg Det[C]
1 71 70.2 97.5 0.67 72.2 96.9 0.69
2 349 64.3 100 0.64 74.8 100 0.75
3 52 92.9 98.5 0.91 96.4 97.8 0.94
4 99 46.2 100 0.46 56.7 99.9 0.57
5 71 90.2 100 0.90 96.9 100 0.97
6 71 96.3 100 0.96 97.5 100 0.98
7 74 90.7 95.4 0.86 91.6 94.0 0.86
8 119 15.1 100 0.15 38.3 100 0.38
9 71 85.9 99.5 0.85 89.8 99.5 0.89
10 71 77.1 91.6 0.69 77.8 89.8 0.68
11 109 92.4 99.7 0.92 94.5 99.5 0.94
12 49 43.1 100 0.43 69.2 100 0.69
13 74 96.9 99.9 0.97 97.6 99.9 0.97
14 74 97.8 100 0.98 98.3 100 0.98
15 90 87.3 100 0.87 86.5 100 0.87
16 75 74.7 100 0.75 84.3 100 0.84
17 72 98.6 98.8 0.97 98.6 98.8 0.97
18 71 81.5 99.8 0.81 88.0 100 0.88
19 71 36.3 100 0.36 37.6 100 0.38
20 71 93.2 37.5 0.31 97.1 36.6 0.34
21 232 83.6 100 0.84 83.4 100 0.83
Average 76.9 96.1 0.73 82.2 95.8 0.78

The performance results are outlined in the table shown above. Three performance measures were computed: correct classification of skin pixels, correct classification of background pixels, and the determinant of the confusion matrix Det[C]. With respect to the Det[C] measure, out of 21 sequences considered, 16 performed better using our dynamical approach. An increase in performance of up to 25% was observed. Performance increase of over 10% was observed on five sequences. Skin classification rates with dynamic histograms were as good or better than the static histogram approach in all cases.

The five sequences that failed to perform better, had an insignificant performance loss. In all five failure cases, the system performed no worse than 1%. This performance degradation was due to skin-like color patches appearing in the background of initial frames of a sequence. Recall that these initial frames are used in in estimating the parameters of the Markov model (see technical report for more details).

Finally, we performed a set of experiments to establish system stability over time. For example, the graph in below shows system performance on the longest sequence in our test set (349 frames).

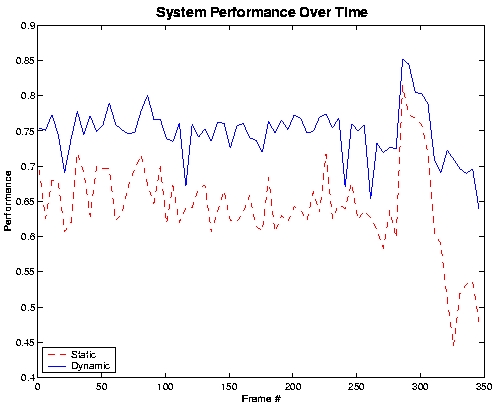
Fig. 3: Performance of the dynamical system over an extended sequence. The horizontal axis represents time, measured in frames. The vertical axis represents the performance measured by the determinant of the confusion matrix. The dotted line corresponds to the performance of the static histogram segmentation, and the solid line to our dynamic approach.

As can be seen from the graph, the dynamic approach was consistently better than the static method in classifying skin and background pixels. Not only does our system perform over 10% better for the entire sequence, it is also more stable. The standard deviation of performance for our system was measured to be 0.0375, which is almost a half of the standard deviation of 0.0630 measured for the static segmentation approach. It should be noted that the stability of our system was consistent across experiments.

© 2000 Image and Video Computing Group - Boston University 
Last Modified: March 14, 2000