1. Using the current IPv4 Internet Protocol, the IP address of a computer connected to the Internet consists of 4 bytes (32 bits). Realizing that we may soon run out of IP addresses to give to all possible computers out there, the IPv6 protocol allows for 16-byte IP addresses.

   1. Under IPv4, how many computers with IP addresses could co-exist on the Internet at any point in time?

   2. Potentially, under IPv6, how many computers with IP addresses could co-exist on the Internet at any point in time?

    

2. Using the IP protocol, information communicated over the Internet is broken down into packets, each of which carrying 1.5KB of data. How many packets would it take to send each of the following on the Internet:
   1. A 140-character tweet on Twitter. Recall that a character can be represented in a single byte.
   2. A 1,600x1,200 bitmap picture with 24-bit color depth. Recall that each pixel in a bitmap picture is represented by three bytes for RGB (hence the 24-bit color depth).
   3. A 3GB movie.

    

3. A friend of yours who has not taken MA/CS-109 is wondering how is it that signals carried by fiber-optic cables, Wi-Fi, wires, satellites, and cell phones are all part of the same Internet. How do you explain to him/her that one does not need to re-engineer the Internet any time a new way to carry signals is invented?

    

4. A friend of yours who has not taken MA/CS-109 is wondering how is it that a network designed to carry text is now being used for music, telephony, photos, video, etc.  After all, the good old telegraph wires could not be used for telephone communication, and telephone wires did not help when TV was invented.  How do you explain to him/her that you do not need to re-engineer the Internet whenever a new application is invented?

    

5. Researchers at Georgia Tech, at UC Berkeley, and at Boston University (among other places) are looking into making the Internet available at very remote/under-developed parts of the world. The main challenge in "connecting" such rural areas is that it is not economically feasible to run wires (coaxial or fiber) or to use satellite communication to remote villages with very sparse population. To solve this problem, these researchers are using buses (yes buses) to move the IP packets between a remote rural area and larger neighboring towns where Internet is available. The bus is literally acting as a wire between the router in the remote village and the router in the neighboring town! Upon hearing about this, a friend of yours who did not take MA/CS-109 wondered about the usefulness of such an approach since in his/her mind, one must re-engineer the whole Internet to allow for buses to ferry packets around!

   How do you explain to your friend that you do not need to re-engineer the Internet whenever a new method of moving packets around is invented?

    

6. Consider the following switching network made up of a 16-to-1 multiplexer connected to a 1-to-16 de-multiplexer.

   

   1. What bits would you provide as the sender address and what bits would you provide as the receiver address to enable Lady W to speak to Lady X?

      Sender Address: _______________

      Receiver Address: _______________

       

   2. With lady W and lady X chatting away, when lady Y tried to speak to lady Z, she got the "all lines are busy" signal. Why did that happen?

       

   3. With phone networks (which are designed using switches as illustrated above), especially around busy periods (e.g., Mother's day), we sometimes run into the same "all lines are busy" problem (even though both ends of the call are not themselves busy).The same is not true with the Internet in the sense that even when loads are high, calls on the Internet are still able to go through (even if the quality of the connection is not that great). What design feature of the Internet (as opposed to the phone network) makes that problem (of "all lines are busy") disappear?

    

7. As discussed in class and explained in the notes, IP addresses of computers on the Internet consist of 4 bytes. If all computers in the computer science department research lab start with the same sequence of bits, namely: 1000000011000101000010. How many different computers could the CS department have on the Internet?

    
8. Label each statement as either "always true", "always false", or "it depends" (i.e., it could go either way depending on other details). 
   • The number of steps of Dijkstra's shortest path algorithm when applied to an arbitrary graph is linear in the number of nodes in the graph.
   • For graph nodes A, B, and C: the cost of the shortest path from A to B is less than or equal to the sum of the costs of the shortest paths from A to C and from C to B.
   • A graph with N nodes can always be colored using N or less colors.
   • If the rate with which cars arrive at a toll booth doubles, then the length of the queue of cars waiting to go through the tolls will also double.
   • If the utilization of a service is 80% and the rate with which requests are made is 40 requests per hour, then the capacity of the service is 50.
   • The Internet protocol guarantees the delivery of every packet it handles.
   • The Internet protocol deals with packets differently depending on whether these packets carry text, audio, video, etc.
   • It is easy to check whether a proposed solution to an NP problem is a correct solution.
   • According to Google’s PageRank algorithm, a web page’s rank is based solely on the total number of links from other pages to that page.
    
9. Earlier this month (April 2010), The Library of Congress (LoC) decided that it will archive all the tweets that were ever tweeted (and will continue to do so for the foreseeable future) – note: A tweet is a message consisting of at most 140 characters.

   Upon hearing this development, a friend of yours who is quite concerned about government spending commented that “this is crazy; the LoC will have to spend a ton of money to store all these tweets.” Follow the steps below to develop a quantitative argument about this issue:

   1. Assuming that an average Twitter user produces 10 tweets per day, how much storage will be needed to preserve the tweets of one account for one year?

   2. Assuming that an individual will tweet for an average of 60 years, how much storage will be needed to preserve the lifetime tweets of all 300 million US citizens (assuming that they all have Twitter accounts)?

   3. Today, it costs around $1 to store 10GB. How much will it cost the LoC to preserve the tweets of all US citizens?

   4. Looking to the future, the LoC will have to preserve the tweets of all future accounts. Considering that there are about 15 births per 1,000 people in the US per year, the number of accounts kept by the LoC will grow by about 1.5% per year. Storage costs, on the other hand are decreasing at a fixed rate per year (about 40% per year for hard disks). Do these rates bode well for the LoC or should they worry about the escalating costs of maintaining all these tweets?

   5. Would your thinking change if you consider the entire world population (as opposed to only US citizens)? Note: In fact, the LoC is archiving all Twitter account tweets (not just those by US citizens).
   6. If government spending is not a concern of yours (or is a non-issue considering your quantitative assessment above), are there other concerns that you should be considered?
    
10. Answer the following questions about the graph abstraction of the DC Metro shown below, where the red dots represent a subset of the stations and the numbers shown represent the number of metro stops between two pairs of stations.

    

     

    1. How many nodes are there in this graph?

    2. How many edges are there in this graph?

    3. Are the edges in this graph directed or not?

    4. What is the maximum degree of any node in this graph? (Hint: The degree of a node is the number of edges from/to that node)

    5. What is the diameter of this graph? (Hint: The diameter of a graph is the length of the longest shortest path between any two nodes)

     

11. Prove that the shortest path between two nodes in a graph with N nodes cannot be more than N-1 in length.

     

12. Consider applying Dijkstra's shortest-path algorithm to the following graph starting with node A.

    

    Recall that Dijkstra's algorithm works iteratively. In each iteration, it augments by one the set of nodes for which a shortest path is already known. For example, in the first iteration (for the above graph), the algorithm will add node "C" since the path to C has the minimum cost (of 3) among all nodes it is yet to reach (B, C, D, and E). In the next iteration, the algorithm will add "B" since the path to B (through C) has the minimum cost (of 4) among all nodes it is yet to reach (B, D, and E). This process goes on until the shortest path to all reachable nodes is found.

    In what order will Dijkstra's algorithm discover the shortest paths between A and the various destination nodes in the graph?

     

13. You are planning a car trip from city A to city B, and you are interested in stopping along the way to visit a friend in city C. You are told that the shortest path between A and B is 135 miles and that the shortest path between A and C is 80 miles. What is your estimate of the shortest path between C and B? Your answer should be in the form: “The shortest path between C and B is (at least, at most, or exactly) … miles long”. In one or two sentences explain your logic.

     

14. Your friend who is a CS major wrote a program to compute the shortest path between a given node in a graph and all other nodes in that graph using Disjkstra’s algorithm. When she ran her program on a graph with 100 nodes, the program took 1 second to run. Can you guess how long her program will take if it is run on a 1,000-node graph? Why?

     

15. Consider three stops A, B, and C on the T subway map. The shortest path between A and B takes 15 minutes and the shortest path between A and C takes 25 minutes. For each of the statements below, state which one is correct (i.e., you can prove it), incorrect (i.e., you can disprove it), or neither.
    • The shortest path between B and C is less than 10 minutes
    • The shortest path between B and C is exactly 10 minutes
    • The shortest path between B and C is more than 10 minutes
    • The shortest path between B and C is at most 10 minutes
    • The shortest path between B and C is at least 10 minutes

     

16. Consider three stops A, B, and C on the T subway map. The shortest path between A and B takes 15 minutes and the shortest path between B and C takes 25 minutes. For each of the statements below, state which one is correct (i.e., you can prove it), incorrect (i.e., you can disprove it), or neither.
    • The shortest path between A and C is less than 40 minutes
    • The shortest path between A and C is exactly 40 minutes
    • The shortest path between A and C is more than 40 minutes
    • The shortest path between A and C is at most 40 minutes
    • The shortest path between A and C is at least 40 minutes

     

17. The Federal Communications Commission (FCC) prevents interference between radio stations by assigning appropriate frequencies to each station. Two stations cannot use the same channel when they are within 150 miles of each other. Use graph coloring to find out how many different frequencies are needed for the six stations located at the distances shown in the table below by following the steps below.

    

     

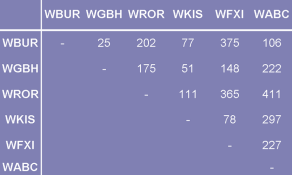
    1. Model the conflict relationships between the above stations with a graph. What do the nodes of the graph represent? What does an edge in that graph represent?

    2. Identify the minimum number of colors needed to color the nodes of the graph you obtained in step (a) such that no two adjacent nodes are assigned the same color.

    3. Use your answer in step (b) to determine the minimum number of frequencies needed for the six stations.

     

18. Consider the following data collected using Traceroute experiments between 3,600 pairs of computers. Answer the following questions:

    

     

    1. What proportion of the sample had between 11 and 14 hops, inclusive?

    2. Can you give a margin of error and a confidence interval for your answer in part a?

    3. What is the chance (probability) that the confidence interval you provided in part b. will not catch the "real" proportion of pairs of computers with a distance between 11 and 14 hops?

     

19. You are starting a new company "AcmeCorp.com" and want to make sure that your competition will not "hijack" your web presence by creating web sites for misspelled versions of "AcmeCorp". Since web site names are case-insensitive, you have to account for a typo in each position of the word "acmecorp". How many web site names would you have to register with the Internet domain name authority to protect yourself from a single typo?

     

20. Using contradiction, make an argument for why the same node X cannot appear twice on the shortest path between any pair of nodes, say A and B. What assumption is necessary for your argument to hold?

     

21. Using induction, prove the following statement: The shortest path between any two nodes in a connected graph with n nodes cannot contain more than  n-1 edges. What assumption is necessary for your argument to hold?

     

22. You have been hired as an intern at a consulting firm who is retained to look at where would be the best places to install Internet kiosks at Disney's Magic Kingdom (or you favorite park). Each one of the k (e.g., k=3) kiosks to be installed needs to be right next to the entrance to a landmark (e.g., a ride or a food court, etc.) The prevailing wisdom in the firm is that the best place for the kiosks would be next to the landmarks that have the most neighboring landmarks, since these are the most “central”. Two landmarks are “neighbors” if there is a way to walk directly from one to the other.  However, having taken MA/CS-109, your intuition is that it is far better to identify the landmarks that are likely to be visited the most, whether or not they are central by virtue of having many other landmarks next to them. You were given the set of landmarks (and the walkways between them) and the percentage of people going from one landmark to every one of its neighbors.

    Answer the following questions:

    1. Show how you could model the flow of people between park landmarks as a graph. In particular, specify what constitutes the nodes of the graph, the edges of the graph, whether the edges are directed or not, and the labels on the edges.

    2. In your own words, explain how you would make the case for a different approach -- in particular an approach that mirrors how Google ranks the various web pages to measure their popularity.

     

23. As part of the recovery act, the small town of Wanderland is slated to receive $1M to upgrade their three town intersections to relieve traffic congestion. To decide how much money to allocate to the upgrade of each intersection, Wanderland collected traffic data, which they represented as a graph in which intersections are nodes and directed edges are streets. The data they collected allowed them to label each edge (street) out of a node (intersection) with the proportion of cars at the intersection that would take that edge. The results they obtained are shown below.

    

    The Wanderland board of selectmen, upon looking at the results noted that since each intersection has the same number of streets into it, decided to split the $1M equally.

     

    1. Explain why just counting the number of roads going into an intersection is not a good measure of whether the intersection may (or may not) be busy.

    2. What process may be used to model how cars go through Wanderland's intersections?

    3. Following the process you adopted in part (b) write down three relationships that would allow you to compute how relatively busy the intersections are.

    4. To explain your ideas to the board of selectmen you decided to simulate the process you adopted in part (b). So, you started with 100 cars in each intersection and proceeded to compute the number of cars in successive one minute intervals (assuming it takes one minute to travel between any two intersections). Show the number of cars in the first minute and in the 1001^st minute of the simulation below.

       Time	@ A	@B	@C
       0	100	100	100
       1
       …
       1000	72.687	121.586	105.727
       1001

        

    5. What criticisms do you expect from the board of selectmen regarding the process you adopted in part (b)? How would you answer them?

     

24. You were hired by a marketing firm and were asked to review the rates that the firm is charging for three special displays at an amusement park. One of these displays is located at the main entrance of the park (location A); the second is located next to the food court (location B), and the third is located next to main ride (location C). Studies of how visitors of the park move from one location to another in a period of 15 minutes suggest that:

    • Of all people in location A: 20% end up going to location B, 50% end up going to location C, and 30% remain in location A.

    • Of all people in location B: 60% end up going to location C, and 40% end up going to location A.

    • Of all people in location C: 30% end up going to location A, and 30% end up going to location A, and 40% remain in location C.

    Given this information, you proposed that a sensible approach to setting the pricing for the special displays is to make the price proportional to the number of people that are expected to be at each one of the three locations.

    1. Show how you could model the flow of people as a graph. In particular, specify what constitutes the nodes of the graph, the edges of the graph, whether the edges are directed or not, and the labels on the edges.

    2. Draw the graph corresponding to the above observations.

    3. If P(A), P(B), and P(C) denote the proportion of the park visitors expected at each one of the three locations (long after the park opens in the morning). Write three relationships that would allow you to figure out these proportions.
        

25. Prove that adding a single edge between two distinct nodes in a Eulerian graph will result in a new graph that is not Eulerian. Hint: Recall that for a Eulerian circuit to exist in a graph, all the nodes of the graph must have an even degree.

     

26. Consider three stops A, B, and C on the T subway map. You are told that:

    • The shortest path between A and B takes 15 minutes
    • The shortest path between B and C takes 25 minutes

    Complete the table below by specifying for each statement whether the statement is correct (i.e., you can prove it), incorrect (i.e., you can disprove it), or neither.

    Statement	Correct? (Yes/No/Maybe)
    The shortest path between A and C is less than 40 minutes
    The shortest path between A and C is exactly 40 minutes
    The shortest path between A and C is more than 40 minutes
    The shortest path between A and C is at most 40 minutes
    The shortest path between A and C is at least 40 minutes

     

27. Facebook is a social networking application that allows individuals to befriend each other. Twitter is a social networking application that allows individuals to “follow” the news (tweets) of one another. One can model each of these applications with a graph. Complete the table below:

    Question	Facebook	Twitter
    What do graph nodes represent?
    What do graph edges represent?
    Are edges directed or undirected?
    What would be a good use of the solution to the shortest-path algorithm on the graph?
    What would be a good use of the solution to the PageRank algorithm on the graph?

     

28. Consider the following word game (called Doublet and proposed by Lewis Carroll in 1879).
    
    You are given two English words of the same length, and you are asked to come up with a sequence of words of the same length starting with the first and ending with the last, such that every word in the sequence is a correct English word (e.g., from the Webster dictionary), and any two consecutive words in the sequence differ in exactly one letter. Such a sequence of words is said to be a “valid sequence”.
    
    For example, if you are given HEAD and TAIL, then HEAD-HEAL-TEAL-TELL-TALL-TAIL is an example of a valid sequence. Clearly there could be many valid sequences from HEAD to TAIL. For example, HEAD-HEAL-DEAL-TEAL-TELL-TALL-TAIL is another one.
    
    You win the game if you can come up with the shortest valid sequence of words.
    
    It was suggested that one strategy to win this game is to use a graph to explore all possible valid sequences from any word in the English dictionary to any other word in the English dictionary.

    1. What should the nodes of the graph represent?

    2. What should the edges of the graph represent?

    3. If you are given two English words, what algorithm would you use on the graph to come up with the winning word sequence?
        

29. Vehicular traffic around the BU Bridge inexplicably grinds to a halt every time there is a red-sox game or there is an event at the Agganis Arena. The root of the problem seems to be that the traffic lights are set on an automatic timer, which in some cases lets too many cars go through one traffic light at an intersection, resulting in the blocking of the intersection, which means that even if a second traffic light at the intersection turns green, vehicles can’t move. This in turn may result in other blockages at other intersections, which (not surprisingly) end up contributing to the initial blockage. To resolve the blockage at one intersection requires the resolution of the blockage at another; yet, to resolve the blockage at that second intersection requires the resolution of the blockage at the first! Situations like this are called “deadlocks”.

    Deadlocks occur when there is a “cycle” of blockages, and this cycle could be of any length (not just two as described above) – i.e., blockage at intersection 1 causes blockage at intersection 2 which causes blockage at intersection 3, …, which causes blockage at intersection m, which causes blockage at intersection 1!

    By programming traffic lights at various intersections in a city center (such as around BU), one can determine if it is ever the case that traffic through one intersection will cause blockage of traffic in another intersection. For a particular city center with 7 intersections, and for a particular setting of the traffic light programming, the following relationships were observed:  

    .	1	2	3	4	5	6	7
    1	.	*	*	*	-	*	-
    2	-	.	*	-	*	-	-
    3	-	-	.	*	-	-	-
    4	-	-	-	.	-	-	-
    5	-	-	-	-	.	-	*
    6	-	-	*	-	*	.	-
    7	-	*	-	-	-	-	.

    In the table above a star in entry row i and column j means that the intersection i could cause blockage at intersection j.

    To visualize these relationships, you decided to use a graph where vertices represent intersections and edges represent blockage relationships.

    1. Draw the graph. Is the graph directed or not?

    2. Show that traffic in the city center could potentially be deadlocked by finding a cycle of blockage dependencies.

    3. Identify the set of intersections whose traffic lights must be reprogrammed to alleviate this deadlock potential.

    Note: You can read more about deadlocks (a classical problem in computer science) at http://mcs109.bu.edu/site/?p=deadlock

     

30. Given the 5-node graph shown, answer the following questions:

     

    1. Write down the degree of each node in the graph. What is the average degree?
    2. What is the probability that a new node (F) will attach itself to node A under the “Random Attachment” growth model?
    3. What is the probability that a new node (F) will attach itself to node A under the “Preferential Attachment” growth model?

     

31. Facebook is a social networking application that allows individuals to befriend each other. Twitter is a social networking application that allows individuals to follow the news (tweets) of one another. One can model each of these applications with a graph.

    Answer the following questions for each one of the above applications:

    1. What would constitute a node in the graph?

    2. What would constitute an edge in the graph?

    3. Are the edges of the graph directed or undirected?

    4. Can you think of a good use of the solution to the shortest path problem between two nodes in the graph? What kind of "social networking" question does it solve?

    5. Can you think of a good use of the solution to the PageRank algorithm  on the graph? What kind of "social networking" question does it solve?

     

32. The “popularity contest” between CNN and Ashton Kutcher on Twitter has focused on who of the two is able to gather more followers. How would you explain to a friend of yours who has not taken MA/CS-109 that a simple count of Twitter followers is not the best way to settle this popularity context?

     

33. Cars arrive at a car wash at an average rate of 10 cars per hours and it takes 5 minutes to wash each car.

    Answer the following questions:

    1. What is the maximum rate with which cars can go through the wash?
    2. What is the utilization of the car wash?
    3. On average, how many cars do you expect to find at the car wash? [Recall that the average size of a queue is given by U/(1-U), where U is the queue utilization]. 

     

34. On a typical day, customers arrive to the post office at an average rate of 8 customers per hour and it takes 5 minutes for the post-office employee to serve each such customer, on average. Answer the following questions:

    1. What is the “capacity” of the post-office – i.e., how many customers would it be possible for the post office employee to serve per hour?  

    2. What is the utilization of the post office on a typical day?

    3. What is the likelihood that a customer will not have to wait in line once they arrive to the post office?  

    4. What is the likelihood that a customer will have to wait in line for more than one person ahead of them? [Hint: You can find this out by calculating the probability that there will be either nobody in line or exactly one other customer in line].

    5. On average, how many customers would be waiting in line on a typical day?

    6. On one of those busy days before Christmas, the rate with which customers arrive to the post office increased by 45%. Repeat parts b, c, d, and e.

     

35. Customers arrive at the line for a fast food restaurant at an average rate of 15 customers per hour and it takes 3 minutes on average to complete the order for each such customer. 

    Answer the following questions:

    1. What is the maximum rate with which the fast food restaurant can serve its customers? In other words, how many customers per hour can the restaurant keep up with?
    2. What is the utilization of the fast food restaurant?
    3. What is the probability that a customer arriving at the fast food restaurant will not have to wait in line for service?
    4. What is the probability that a customer arriving at the fast food restaurant will find exactly 2 other customers in the store?
    5. On average, how many customers would one expect to find in the restaurant?
    6. An advertisement campaign resulted in a 20% increase in the popularity of the fast-food restaurant. Repeat parts b, c, d, and e.

     

36. When you mentioned to your parents that you won't be able to make it home early for the holidays, they were quite annoyed and suggested that BU was not doing a good job scheduling the exams. As an MA/CS-109 graduate, you want to explain to your parents that the problem of scheduling the exams is not as simple as it sounds. In particular, two courses cannot have their exams at the same time if any student is enrolled in both.  Moreover, given enrollment data, figuring out the schedule that minimizes the total number of exam slots is computationally intensive.

    To explain this to your parents, you decided to map the problem to a graph coloring problem whereby the number of colors used to color the graph represent the number of distinct exam slots needed for finals. For example, assuming AM and PM slots for exams per day, Red = Monday AM, Blue = Monday PM, Green = Tuesday AM, etc.

     

    1. What do the nodes in your graph represent?

    2. What do the edges in your graph represent?

    3. For a set of 5 classes, what is the maximum number of exam slots needed? Draw an example graph that requires that number of slots.

    4. To explain the concept, you used the 6 classes that a group of 5 friends are taking in the current semester as an example. Friend #1 is in courses A, B, and C.  Friend #2 is in A, B, and D. Friend #3 is in B, C, and E. Friend #4 is in B, C, and F. Friend #5 is in B, D, and F. Find the minimum number of exam slots in this example (you need to draw and color a graph model of this example).

    You explained to your parents that, in general, to figure out the minimum number of exam slots, one would need to check every possible assignment of classes to slots.  For example, to figure out if 3 classes (A, B, and C) can fit in 2 slots (AM and PM), one would need to check a total of 8 possible schedules for conflicts, since A can be either AM or PM, and for each one of these choices, B can be either AM or PM, and for each one of these choices, C can be either AM or PM. Thus in total one would have to check 2*2*2=8 possible schedules for conflicts. 

    5. You want to convince your parents that doing the above is just too much work. So, you decide to go for more realistic numbers. How many schedules would have to be checked for conflicts if the number of classes is 10? How many would have to be checked if the number of classes is 30? What is the formula for N classes? What kind of function is that?

    6. Now, to impress your parents even more (and convince them that taking MA/CS-109 was worth delaying coming home late for the holidays), you decided to tell them that graph coloring is an example of the "NP" class of problems in Computer Science. In a few sentences, explain what it means for a problem to be labeled as such. What other problems can you mention to them as belonging to the same class? 

     

37. You were hired as a consultant to help look for ways to improve the operation of a tropical fish farm in Florida. The farm raises six different types of tropical fish, each identified by a letter: A, B, C, D, E, and F.  Because of predator-prey relationships, water conditions, and size, some fish can be kept in the same tank, while others cannot. The following table shows which fish cannot be together -- i.e., they have to be shipped in different tanks/containers. For example, fish of type A cannot be in a tank containing fish of type B or fish of type C.  

    Fish Type	A	B	C	D	E	F
    Cannot be with	B,C	A,C,E	A,B,D,E	C,F	B,C,F	D,E

    Every week, the farm arranges for a shipment of fish to a major pet store chain in the Northeast. The price of shipping a single container is $500 and the farm current practice is to ship each type of fish in a separate container, which implies a cost of $3,000 per week (for 6 containers) or $156,000 per year.

    Upon reviewing these facts, you realized that this problem is not very different from many of the problems you have encountered in MA/CS-109, in which graph coloring was used to identify the minimum number of groupings of vertices so that no two vertices with a conflict relationship are put in the same group. Thus, you decided to use graph coloring to figure out a more effective shipping strategy. Answer the following questions:

    • Draw the conflict graph. What do the vertices represent? What do the edges of the graph represent?

    • Based on the conflict graph you obtained, what is the minimum number of tanks needed to ship the fish?

    • How much money would this new shipment strategy save the farm business per year?

38. A friend of yours working as a work-study in the chemistry department was asked to come up with a schedule for their wet labs. Seven courses in the department require the use of the lab once a week and the department would like to have the lab open for the least number of days possible. However, to be considerate, the department also wants to avoid having a student do lab work for more than one course on the same day. In the table below a star in entry row i and column j means that course i and course j have at least one student in common, so labs for these courses should not be scheduled on the same day.

    .	1	2	3	4	5	6	7
    1	.	*	*	*	-	*	*
    2	*	.	*	-	-	-	*
    3	*	*	.	*	-	-	-
    4	*	-	*	.	*	*	-
    5	-	-	-	*	.	*	-
    6	*	-	-	*	*	.	*
    7	*	*	-	-	-	*	.

    Knowing that you took MA/CS-109, your friend asked you for help. After thinking about it for a bit, you realized that this problem is similar to the problem of minimizing the number of tables at a wedding party, given a list of pairs of guests who cannot be seated together. In particular, you recalled that this problem was solved by modeling it as a graph coloring problem.

    1. Model the lab scheduling problem as a graph. In particular, identify what constitutes a vertex in the graph and what constitutes an edge.

    2. Show how you could come up with a schedule by coloring the vertices of the graph.

    3. Are you certain that the schedule you obtained will minimize the number of days when the lab is open? Would you be able to give the same answer for any arbitrary graph? Explain why or why not.

     

39. A directed graph is a graph in which edges are directional, in the sense that you can traverse them in one way but not the other. A cycle exists in a directed graph if one can find a path that goes through a vertex twice. A directed graph is called acyclic if it has no cycles in it.

    Many interesting questions related to real-world problems could be answered by modeling the real-world as a directed graph and by finding if cycles exist in such a graph (e.g., finding if deadlocks may materialize across a number of intersections, detecting if a set of routers on the internet may end up sending traffic destined to a particular target computer in endless loop, detecting if a set of programs on your PC will wait for one another indefinitely causing your computer to inexplicably “hang”, …)

    1. Prove or disprove the following conjectures: "The maximum length of any path in an acyclic graph with N vertices is N-1."

        

    2. Prove or disprove the following conjecture: "In an acyclic graph, there must exist at least one vertex without any outgoing edges."

        

    3. To decide whether a graph has a cycle, the following algorithm was proposed:

       CheckForCycles(G)

       1. For each vertex in the graph G, count the number of outgoing edges.

       2. Find the vertex v with the minimum number of outgoing edges.

       3. If v has any outgoing edges, then print "Cycle Detected" and stop.

       4. Otherwise, obtain a new graph G' by removing v from G, along with any edges connecting any other vertex u to v. Now CheckForCycles(G').

        Explain the logic behind the above algorithm.

    4. If each of the steps in the above algorithm take at most 1 second, show that for any graph with N vertices, the above algorithm will stop in no more than 4*N seconds.

        

    5. Try the above algorithm on the following graph:

       

     

40. A smaller variant of the Sudoku puzzle is called Shudoku. In Shudoku, you are given a 4x4 square (see below), and you are asked to fill every one of the 16 cells with a number so that

    • all numbers in the same row must be distinct

    • all numbers in the same column must be distinct

    • all numbers in any 2x2 quadrants must be distinct

    The trick is to find the minimum set of numbers that make this possible.

    The following is an example of a Shudoku puzzle (in which some of the numbers are already assigned to cells).

    

    To solve the above Shudoku puzzle (or any other), it was suggested that the puzzle be modeled using a conflict graph, where nodes are cells and edges (i.e., conflicts) exist between any two nodes (i.e., cells) that cannot be assigned the same number. 

    Answer the following questions:

    1. How many total nodes are there?

    2. Are the edges of the graph directed or not?

    3. List all the nodes that will be adjacent to the top-left cell.

    4. What is the degree of each node in the graph? In other words, how many edges will each node have?

    5. In one or two sentences, explain why a solution to the graph coloring problem for the graph obtained in step (a) should be a correct solution for the Shudoku puzzle.

    6. Consider a variation of the Shudoku puzzle, in which in addition to the rules of no repeated numbers in the same row, column, or quadrant, we add the rule: all numbers in the 2x2 center square must be distinct. Can you still use graph coloring to solve this new version? Justify your answer (e.g., by showing what modification would be needed to the steps above, or by explaining why graph coloring cannot be used to solve the new puzzle).

     

41. The Audubon society is pursuing a wildlife preservation project and needs to deploy a team of 100 volunteers to sample the number of birds from some species. The birds are known to congregate in three primary locations: A, B, and C.

    In preparation for this project, a team of scientists tagged a small number of birds and determined that the flying patterns of the tagged birds are as follows:

    •   40% of birds in location A were observed one hour later in location B
    •   40% of birds in location A were observed one hour later in location C
    •   50% of birds in location B were observed one hour later in location A
    •   50% of birds in location B were observed one hour later in location C
    • 100% of birds in location C were observed one hour later in location A

    Answer the following questions:

    1. One proposal to the Audubon society was to dispatch an equal number of volunteers to all three locations. Explain why such an approach may result in a biased sampling of the bird population. How should the Audubon society dispatch volunteers to mitigate this bias? [Hint: To ensure that the sampling process is as close as possible to simple random sampling, it is desirable that the number of volunteers dispatched to a location be proportional to the number of birds expected at that location.]

    2. Represent the flying patterns of tagged birds as a graph. What do the nodes in your graph represent? What do the edges represent? Are the edges directed or not?

    3. What process might be used to model the movement of birds between the three locations? In one or two sentences explain in plain English what that process means.

    4. Explain how the above process can be used to help the Audubon society decide on the number of volunteers to deploy to each location.

    5. Write down a set of equations that might be used by the Audubon society to determine the proportion of volunteers to dispatch to each location.

    6. An intern was asked to solve the set of equations in part (e) and to propose how to dispatch 100 volunteers accordingly. Her answer was that 50 volunteers should be dispatched to A, 20 to B, and 30 to C. Do you agree with her conclusion? Explain why or why not. [Hint: You may solve the equations and use the solution to figure out the number of volunteers accordingly, or you may use simulation of the process proposed in part (c).]

     

42. Coming Soon!

Azer Bestavros (2010-12-16)