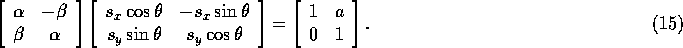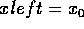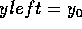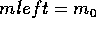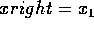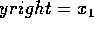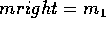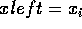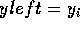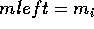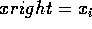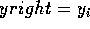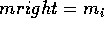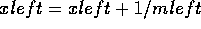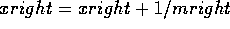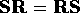BU CLA CS 480: Introduction to Computer Graphics

Spring 1995

Solutions to Homework Assignment 1

1. We need to show that , only if 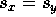, or 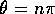for integer values of n. Start by multiplying the matrices:

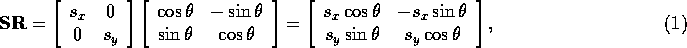
and

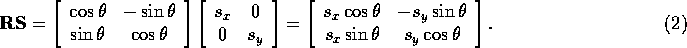
If 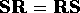, then clearly

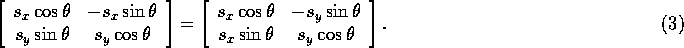
Note that the diagonal elements of both matrices are the same, while the off-diagonal elements are different. This means that for the matrices to be equal, it must be the case that

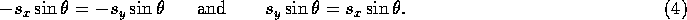
This will be true when 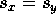, or when 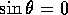(which happens only when 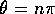for integer values of n). Otherwise, the off diagonal elements of the matrices will not be equal, and therefore .

2. We want to determine the transformation matrix for a reflection around an arbitrary line y = mx + b. One way to solve this is to translate and rotate the problem into an easier coordinate system. If we translate and rotate the line to align it with the x axis, then we can employ the standard transform for reflection about the x-axis.

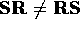The homogeneous coordinate representation is more convenient here because we need to include translation in our formulation. Thus we can build a general reflection about a line as a concatenation of linear transforms. We begin by translating to the line's y intercept to the origin using a translation matrix:

We then need to rotate the line to align it with the x axis:

The sine and cosine for alignment can be found directly from the line equation:

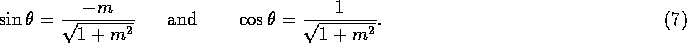
Now that we have a way to get between the line's coordinate system and the world coordinate system, we can employ reflection about the x-axis:

We then inverse rotate, back into the line's orientation:

And finally, translate from the origin back to the line's y intercept:

Thus we build our arbitrary reflection as a concatenation of transforms. We first align the coordinate system of the line with the x axis, we then reflect, and then we return to the original coordinate system:

3. (extra credit) In this problem, we need to find a concatenation of basic linear transforms (rotations, scalings, or translations) that is equivalent to the x-direction shearing matrix. The solution to this problem requires two rotations and one scale:

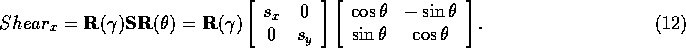
Multiplying out 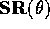we get

We want to find 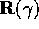that rotates 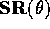into the x shear matrix:

In general, multiplying by a rotation matrix takes the form:

 

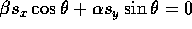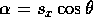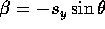The lower left corner of the resulting shear matrix must satisfy . This means that and . Therefore the angle for the second rotation matrix is , and we need to scale the whole system by 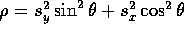. We can now rewrite in terms of this rotation and scaling:

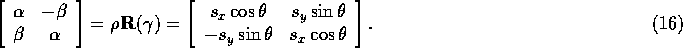
Plugging into Equation 15 and multiplying out, we get:

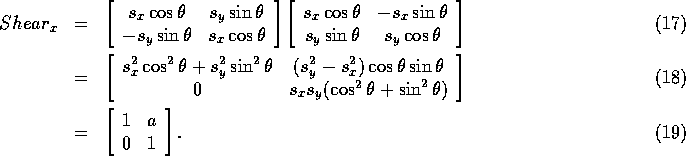
This gives us the equations:

 

 

 

From Equation 22, we see that 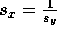. By plugging this into Equation 20, we find that

This holds true when 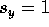or 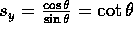. We prefer the case when 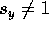, and plug into Equation 21:

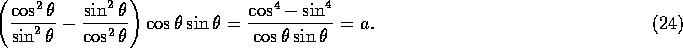
Using trigonometric identities, we find that

This means that

In summary, the x direction shear matrix can be written:

where

4. The following is pseudocode to handle a convex quadrilateral. Note that we would need to handle the special cases of concave or bow-tie quadrilaterals by dividing them into triangles, and calling a triangle scan-fill routine.

 
	discard horizontal edges

	sort remaining edges into a table using lower end point

	(sort by increasing y, and then increasing x)

	find ymin and ymax for the quadrilateral

	for each edge i in the table

		find , the maximum y value for the edge

		find , the x value at the edge's lower end point

		find the slope  for the edge

	end

	

	

	

	

	

	

	i=2

	for y=ymin; y < ymax; y = y+1 do

		for x=xleft; x<=xright; x = x+1

 			write_pixel(x,y,color)

		 if yleft == y then  replace left edge with next active edge

		 	

		 	

		 	

		 	i = i+1

		end

		if yright == y then  replace right edge with next active edge

		 	

			

		 	

		 	i=i+1

		end

		

		

	end

	for x=xleft; x<=xright; x = x+1

		write_pixel(x,ymax,color)

		

Stan Sclaroff 

Created:  February 20, 1995