Problem Set 5

due by 11:59 p.m. on Friday, October 23, 2020

Preliminaries

In your work on this assignment, make sure to abide by the collaboration policies of the course.

If you have questions while working on this assignment, please come to office hours, post them on Piazza, or email cs112-staff@cs.bu.edu.

Make sure to follow the instructions outlined at the end of Part I and Part II when submitting your assignment.

Part I

45 points total

Creating the necessary file

Problems in Part I will be completed in a single PDF file. To create it, you should do the following:

1. Open the template that we have created for these problems in Google Docs: ps5_partI

2. Select File->Make a copy..., and save the copy to your Google Drive using the name ps5_partI.

3. Add your work to this file.

4. Once you have completed all of these problems, choose File->Download->PDF document, and save the PDF file on your machine. The resulting PDF file (ps5_partI.pdf) is the one that you will submit. See the submission guidelines at the end of Part I.

Problem 1: A method that makes multiple recursive calls

10 points; individual-only

A number of the algorithms that we consider in CS 112 involve recursive methods in which a given invocation of the method may make two or more recursive calls. To understand how this type of algorithm works, it helps to draw a call tree for a given set of initial parameters.

In this problem, you will draw such a call tree to illustrate the execution of a simple recursive method that operates on integers. You may find it helpful to review our solutions to the similar problem in Lab 6 problem before continuing.

Here is the method you will trace:

public static int foo(int x, int y) {
    if (y == 0) {
        return x;
    } else if (x <= y) {
        return y;
    } else {
        int result1 = foo(x - 1, y - 1);
        int result2 = foo(x - 1, y + 1);
        return result1 + result2;
    }
}

Assume that we begin with the following initial call to this method:

foo(5, 3)

1. Construct a call tree that shows each invocation of the method, and that uses lines to connect a given invocation to the recursive calls that it makes (if any). Follow the same format that we use in our solutions for Lab 6, Task 2.

   In section 2-1 of ps5_partI, we have given you an initial diagram.

   You should take the following steps to complete it:

   • Add each subsequent call with its parameters to the call tree in the appropriate place.

   • If a given call is a base case, simply put its return value under the call, as we do in our Lab 6, Task 2 solution for calls to fib(1) and fib(0).

   • If a given call is not a base case, use lines composed of / or \ characters to connect the call to the recursive call(s) that it makes.

   • Precede each call with a number that indicates the overall order in which the calls were made.

2. Underneath your call tree, list the order in which the calls return, as well as their return values. When you refer to a given call in this part of the problem, use its number from the call tree.

   For example, the initial call always returns last, so the last line in this part of the problem should look like this:

   call 1 (foo(5,3)) returns ...
   

   where you replace the ... with its return value.

   See our solution for Lab 6, Task 2 for another example of what this part of your solution should look like.

Problem 2: Computing Big-O

10 pts. total; individual-only

1. Express each of the following functions using Big-O notation. Represent your answer as an equality (e.g., p(n) = O(n^2)). The answer for function a(n) is given.

   • a(n) = 8n + 3 = O(n)
   • b(n) = 12n + n^2 + 64
   • c(n) = 2log(n) + n
   • d(n) = log(n) + 2
   • e(n) = 2n

2. Using Big-O notation, determine the number of times the function count is called when the following code fragment runs, in terms of the variable n.

   for (int i = 0; i < n; i++)
       for (int j = 0; j < n; j++)
           for (int k = 0; k < j; k++)
               count();
   

3. Using Big-O notation, determine the number of times the function count is called when the following code fragment runs, in terms of the variable n.

   for (int i = n; i > 0; i/=2)
       for (int j = 0; j < n; j++)
           for (int k = 0; k < 1000; k++)
               count();
   

Problem 3: Sum generator

16 points total; 4 points each part; individual-only

Let’s say that you want to implement a method generateSums(n) that takes an integer n and generates and prints the results of the following series of sums:

1
1 + 2
1 + 2 + 3
...
1 + 2 + ... + n

For example, generateSums(4) should print the following:

1
3
6
10

and generateSums(6) should print the following:

1
3
6
10
15
21

One possible implementation of this method is the following:

public static void generateSums(int n) {
    for (int i = 1; i <= n; i++) {
        int sum = 0;
        for (int j = 1; j <= i; j++) {
            sum = sum + j; // how many times is this executed?
        }
        System.out.println(sum);
    }
}

1. Derive an exact formula for the number of times that the line that increases the sum is executed, as a function of the parameter n.

2. What is the time efficiency of the method shown above as a function of the parameter n? Use big-O notation as we did in lecture, and explain your answer briefly.

   Important

   When big-O expressions are called for in this and future problems, please use them to specify tight bounds as we’ve done in lecture.

3. Create an alternative implementation of this method that also uses iteration (i.e., you should not use recursion) but that has a better time efficiency.

4. What is the time efficiency of your alternative implementation as a function of the parameter n? Use big-O notation as we did in lecture, and explain your answer briefly.

Problem 4: Comparing two algorithms

9 points; individual-only

Suppose that you want to find the largest element in an unsorted array of n elements. Algorithm A searches the entire array sequentially and keeps track of the largest element seen thus far. Algorithm B sorts the array using bubblesort, and then reports the last element as the largest.

1. What is the big-O time efficiency of Algorithm A in the best, average, and worst cases? Explain your answer briefly. (You do not need to implement either algorithm. We just want you to analyze them.)

2. What is the big-O time efficiency of Algorithm B in the best, average, and worst cases? Explain your answer briefly.

3. Which algorithm is faster? Explain briefly.

Submitting your work for Part I

Note: There are separate instructions at the end of Part II that you should use when submitting your work for that part of the assignment.

Submit your ps5_partI.pdf file using these steps:

1. If you still need to create a PDF file, open your ps5_partI file on Google Drive, choose File->Download->PDF document, and save the PDF file on your machine.

2. Login to Gradescope by clicking the link in the left-hand navigation bar, and click on the box for CS 112.

3. Click on the name of the assignment (PS 4: Part I) in the list of assignments on Gradescope. You should see a pop-up window labeled Submit Assignment. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

4. Choose the Submit PDF option, and then click the Select PDF button and find the PDF file that you created. Then click the Upload PDF button.

5. You should see a question outline along with thumbnails of the pages from your uploaded PDF. For each question in the outline:

   • Click the title of the question.
   • Click the page(s) on which your work for that question can be found.

   As you do so, click on the magnifying glass icon for each page and doublecheck that the pages that you see contain the work that you want us to grade.

6. Once you have assigned pages to all of the questions in the question outline, click the Submit button in the lower-right corner of the window. You should see a box saying that your submission was successful.

Part II

55 points total

Problem 5: A Sudoku solver

35 points; individual-only

In this problem, you will write a program that solves Sudoku puzzles using recursive backtracking.

Overview
A Sudoku puzzle consists of a 9x9 grid in which some of the cells have been filled with integers from the range 1-9. To solve the puzzle, you fill in the remaining cells with integers from the same range, such that each number appears exactly once in each row, column, and 3x3 subgrid.

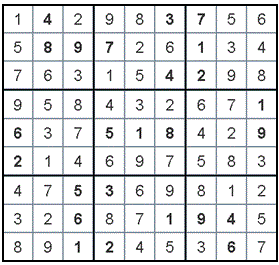
Here is an example of an initial puzzle:

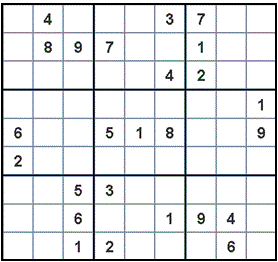
and here is its solution:

Most of the functionality of your program should go in a class called Sudoku, which you will use to represent an individual Sudoku puzzle. We have provided you with skeleton code for this class in the file Sudoku.java, which you should download and modify.

The provided code includes:

• a field called grid that refers to a two-dimensional array of integers. This array will be used to store the current contents of the puzzle, such that grid[r][c] stores the current value in the cell at row r, column c of the puzzle. A value of 0 is used to indicate a blank cell.

• a field called valIsFixed that refers to a two-dimensional array of booleans. It is used to record whether the value in a given cell is fixed (i.e., part of the original puzzle). valIsFixed[r][c] is true if the value in the cell at row r, column c is fixed, and false otherwise. in that cell is not fixed. For example, in the original puzzle above, there is a fixed 4 in the cell at row 0, column 1 (the second cell in the top row), and thus valIsFixed[0][1] would be true for that puzzle.

• a field called subgridHasVal that refers to a three-dimensional array of booleans. This array allow us to determine if a given 3x3 subgrid of the puzzle already contains a given value. For example, subgridHasVal[0][0][7] will be true if the 3x3 subgrid in the upper-left corner of the board (a subgrid that we identify using the indices [0][0]) already has a 7 in one of its cells. See the comments accompanying this field for information about how the subgrids are numbered.

• partial implementations of methods called placeVal() and removeVal() that place a value in a given cell and remove a value from a given cell by updating the fields of the called Sudoku object. You will need to add code to these methods to update any new fields that you add.

• a full implementation of a method called readConfig() that takes a Scanner as its only parameter and reads in a initial configuration of a Sudoku puzzle from that Scanner. This method assumes that this configuration consists of nine lines of text — one for each row of the puzzle — and that each line contains nine integers separated by whitespace, with 0 used to indicate a blank cell. For example, the initial configuration of the puzzle above would begin:

  0 4 0 0 0 3 7 0 0
  0 8 9 7 0 0 1 0 0
  ...
  

  The method reads in the puzzle configuration and updates the called object accordingly. You should not need to change this method, because it calls placeVal(), and you are already modifying that method as needed. However, we do recommend that you read and understand this method.

• the full implementation of a method called printGrid() that prints out the current contents of the grid belonging to the called Sudoku object.

• the skeleton of a method called solveRB() that you will implement. This is the key recursive-backtracking method, and it should return true if a solution is found to the puzzle represented by the called Sudoku object, and false if no solution has yet been found (i.e., if the method is backtracking). If the initial call to this method returns false, that means that the initial puzzle is not valid, and therefore no solution can be found. If there is more than one solution (which can happen if the puzzle doesn’t have enough numbers in its initial configuration), your code should stop after finding one of them.

  The method takes a parameter n, which is the number of the cell that the current invocation of this method is responsible for. We recommend that you consider the cells one row at a time, from top to bottom and left to right, which means that they would be numbered as follows:

  0  1  2  3  4  5  6  7  8
  9 10 11 12 13 14 15 16 17
  ...
  

  Important notes:

  • Make sure that your solveRB() method uses the placeVal() and removeVal() methods when updating the state of the puzzle.

  • Make sure that you don’t attempt to assign a new number to cells that are filled in the original puzzle — i.e., cells whose values are fixed. Your solve() method will need to skip over these cells somehow.

• a full implementation of a “wrapper” method called solve() that makes the initial call to solveRB(), and that returns the same value that solveRB() returns. You should not change this method.

• the skeleton of a constructor. You should add the code needed to initialize the additional fields that you add.

• a main() method that will be executed when you run your Sudoku solver. You shouldn’t need to change this method, but we encourage you to review its use of the methods of the Sudoku class. In particular, note that it displays the puzzle after the solution is found, and thus it isn’t necessary for your recursive-backtracking method to display it.

Adding fields and methods
In addition to completing the methods mentioned above, you should also add to the Sudoku class whatever additional fields or methods are needed to maintain the state of a Sudoku puzzle and to solve it using recursive backtracking.

To determine what additional fields are needed, ask yourself: What other fields do I need to be able to efficiently check the constraints of the puzzle – i.e., to determine whether a given value can be placed in a given cell? See our n-Queens solver for for another example of efficient constraint checking.

For full credit, your constraint-checking must be done without scanning through the rows and columns of the Sudoku board. For example, to determine if the current column contains a 5, you should not need to look at the other cells in the current column.

Make sure that you modify the placeVal() and removeVal() methods so that they correctly update the fields that you add. In addition, make sure that you employ proper encapsulation.

Sample puzzles

• puzzle1.txt

• puzzle2.txt

• no_solution.txt, which has no solution

• multi_sol.txt, which has multiple solutions

A sample run of the program is shown below.

Enter the name of the puzzle file: puzzle1.txt

Here is the initial puzzle:
-------------------------------------
|   | 4 |   |   |   | 3 | 7 |   |   |
-------------------------------------
|   | 8 | 9 | 7 |   |   | 1 |   |   |
-------------------------------------
|   |   |   |   |   | 4 | 2 |   |   |
-------------------------------------
|   |   |   |   |   |   |   |   | 1 |
-------------------------------------
| 6 |   |   | 5 | 1 | 8 |   |   | 9 |
-------------------------------------
| 2 |   |   |   |   |   |   |   |   |
-------------------------------------
|   |   | 5 | 3 |   |   |   |   |   |
-------------------------------------
|   |   | 6 |   |   | 1 | 9 | 4 |   |
-------------------------------------
|   |   | 1 | 2 |   |   |   | 6 |   |
-------------------------------------

Here is the solution:
-------------------------------------
| 1 | 4 | 2 | 9 | 8 | 3 | 7 | 5 | 6 |
-------------------------------------
| 5 | 8 | 9 | 7 | 2 | 6 | 1 | 3 | 4 |
-------------------------------------
| 7 | 6 | 3 | 1 | 5 | 4 | 2 | 9 | 8 |
-------------------------------------
| 9 | 5 | 8 | 4 | 3 | 2 | 6 | 7 | 1 |
-------------------------------------
| 6 | 3 | 7 | 5 | 1 | 8 | 4 | 2 | 9 |
-------------------------------------
| 2 | 1 | 4 | 6 | 9 | 7 | 5 | 8 | 3 |
-------------------------------------
| 4 | 7 | 5 | 3 | 6 | 9 | 8 | 1 | 2 |
-------------------------------------
| 3 | 2 | 6 | 8 | 7 | 1 | 9 | 4 | 5 |
-------------------------------------
| 8 | 9 | 1 | 2 | 4 | 5 | 3 | 6 | 7 |
-------------------------------------

Problem 6: Coming soon

20 points; pair-optional

This is the only problem of the assignment that you may complete with a partner. See the rules for working with a partner on pair-optional problems for details about how this type of collaboration must be structured.

TBA

Submitting your work for Part II

You should submit only the following files:

• Sudoku.java
• TBA

Make sure that you do not try to submit a .class file or a file with a ~ character at the end of its name.

Here are the steps:

1. Login to Gradescope as needed by clicking the link in the left-hand navigation bar, and then click on the box for CS 112.

2. Click on the name of the assignment (PS 4: Part II) in the list of assignments. You should see a pop-up window with a box labeled DRAG & DROP. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

3. Add your files to the box labeled DRAG & DROP. You can either drag and drop the files from their folder into the box, or you can click on the box itself and browse for the files.

4. Click the Upload button.

5. You should see a box saying that your submission was successful. Click the (x) button to close that box.

6. The Autograder will perform some tests on your files. Once it is done, check the results to ensure that the tests were passed. If one or more of the tests did not pass, the name of that test will be in red, and there should be a message describing the failure. Based on those messages, make any necessary changes. Feel free to ask a staff member for help.

   Note: You will not see a complete Autograder score when you submit. That is because additional tests for at least some of the problems will be run later, after the final deadline for the submission has passed. For such problems, it is important to realize that passing all of the initial tests does not necessarily mean that you will ultimately get full credit on the problem. You should always run your own tests to convince yourself that the logic of your solutions is correct.

7. If needed, use the Resubmit button at the bottom of the page to resubmit your work. Important: Every time that you make a submission, you should submit all of the files for that Gradescope assignment, even if some of them have not changed since your last submission.

8. Near the top of the page, click on the box labeled Code. Then click on the name of each file to view its contents. Check to make sure that the files contain the code that you want us to grade.