Lab 12: 2-3 trees; binary-tree iterators

Task 1: Work with 2-3 trees

Your work for this task should be done on paper. Please show your work to a staff member before you leave the lab.

As discussed in lecture, a 2-3 tree is a search tree that is guaranteed to always be balanced, which ensures that all of the key operations will have a worst-case time complexity of O(log n), where n is the number of items in the tree.

1. Create a 2-3 tree from the following sequence of keys:

   45, 1, 25, 12, 26, 44, 4, 50, 43, 21
   

2. What does the tree look like after the following operations?

   • insert 5
   • insert 42

3. What items do I have to visit if I’m searching for an item with each of the following keys?

   • 44
   • 18

Task 2: Understand and design a binary-tree iterator

Preliminaries

Consider the following binary tree (which is not a binary search tree):

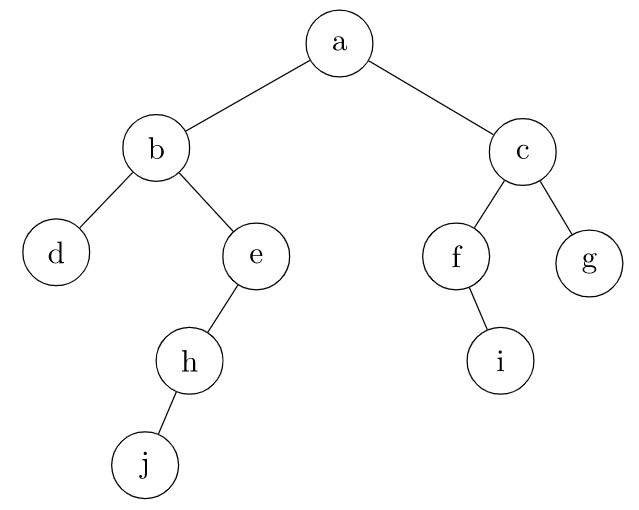
0. Say that we want to traverse the tree and print the keys in each of the nodes. What will the output be if we use a preorder traversal?

In lecture, we performed our tree traversals using recursive methods. However, those traverals were limited in two important ways:

• They always processed the entire tree all at once.

• They required methods that were part of the LinkedTree class, and they were limited to whatever processing those methods performed. (In our case, they were limited to printing the keys.)

To allow a client to flexibly and gradually process the keys in a binary tree in whatever way they choose, we’d like to provide an iterator for a binary tree.

Much like a linked-list iterator, a binary-tree iterator gives a client access to the items in a collection one at a time. Since there are different ways to traverse a binary tree, an iterator could be designed for each type of traversal.

In Problem Set 8, you will implement an iterator that performs an inorder traversal. In this lab, we’ll discuss the implementation of an iterator that performs a preorder traveral.

A need for parent references

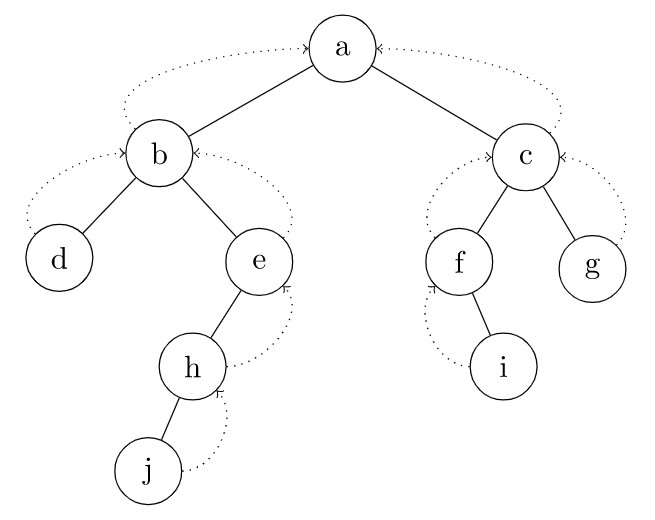
Before we go any further, we need to mention a related change to the LinkedTree class that is needed to implement iterators. We need to add a parent field to each node in the tree; it will be used to hold a reference to the node’s parent. Below is an example of a tree in which these references have been added. They are shown as arrows that have dotted lines.

In Problem Set 8, you will need to modify the LinkedTree code so that these parent references are correctly maintained. For the sake of this exercise, we will assume that these references are already fully supported.

The interface and the beginnings of the class

The Java class for our tree iterator should implement the following interface:

public interface LinkedTreeIterator {
    // are there other nodes to see in this traversal?
    boolean hasNext();

    // return the value of the next node in the traversal, 
    // and advance the position of the iterator
    int next();
}

Given an object called iter of a class that implements this interface, we will be able to use the following code to process all of the keys in the tree that the iterator is associated with:

while (iter.hasNext()) {
    int key = iter.next();
    // process the value of key in whatever way you choose
}

Each type of iterator will be implemented as a private inner class of the LinkedTree class. If we name the class for our preorder iterator PreorderIterator, the header of the class will look like this:

public class LinkedTree {
    ...
    private class PreorderIterator implements LinkedTreeIterator {
        ...

1. What field(s) do we need in our PreorderIterator class?

2. What should the constructor for the class do?

3. What should the hasNext() method look like?

The next() method

The next() method in our iterator class must do two things:

• It must return the value of the next node to be visited (in this case, the value of the node’s key).

• It must advance the iterator so that it is ready for the next call to this method.

Note that the method cannot do work after returning, so the value of the next node must be saved before the iterator’s state is updated.

4. If there are no additional nodes to visit, what should we do?

5. The second task involves updating the state of the iterator. What variable or variables should be updated?

6. In order to accomplish the first task, what do we need to do before updating the iterator’s state?

7. When advancing the iterator, there are several possible cases that need to be handled. These cases depend on the number and types of children of the node whose key we are about to return (which we will call the “current node”).

   Looking at our earlier example, what are these cases, and how would you advance the iterator in each case?

8. Once the iterator has been advanced, what final thing needs to be done?