Problem Set 8

due by 11:59 p.m. on Tuesday, May 3, 2022

Preliminaries

In your work on this assignment, make sure to abide by the collaboration policies of the course.

If you have questions while working on this assignment, please come to office hours, post them on Piazza, or email cs112-staff@cs.bu.edu.

Make sure to submit your work following the instructions found at the end of the assignment.

Part I

40 points total

Creating the necessary folder

Create a subfolder called ps8 within your cs112 folder, and put all of the files for this assignment in that folder.

Creating the necessary file

Problems in Part I will be completed in a single PDF file. To create it, you should do the following:

1. Access the template that we have created by clicking on this link and signing into your Google account as needed.

2. When asked, click on the Make a copy button, which will save a copy of the template file to your Google Drive.

3. Select File->Rename, and change the name of the file to ps8_partI.

4. Add your work for the problems from Part I to this file.

5. Once you have completed all of these problems, choose File->Download->PDF document, and save the PDF file in your ps8 folder. The resulting PDF file (ps8_partI.pdf) is the one that you will submit. See the submission guidelines at the end of Part I.

Problem 1: Checking for keys above a value

10 points total; individual-only

The code below represents one algorithm for determining if there are any keys greater than a given value v in an instance of our LinkedTree class. The anyGreaterInTree() method returns true if there are any keys greater than v in the tree/subtree whose root node is specified by the first parameter of the method, and it returns false if there are no such keys. The anyGreater() method returns true if there are any keys greater than v in the entire tree represented by the LinkedTree object on which the method is invoked and false otherwise.

public boolean anyGreater(int v) {
    // make the first call to the recursive method,
    // passing in the root of the tree as a whole
    return anyGreaterInTree(root, v);
}

private static boolean anyGreaterInTree(Node root, int v) {
    if (root == null) {    
        return false;
    } else {
        boolean anyGreaterInLeft = anyGreaterInTree(root.left, v);
        boolean anyGreaterInRight = anyGreaterInTree(root.right, v);
        return (root.key > v || anyGreaterInLeft || anyGreaterInRight);
    }
}

1. For a binary tree with n nodes, what is the time efficiency of this algorithm as a function of n? Use big-O notation, and explain your answer briefly.

   If the time efficiency depends on the keys in the tree or on the tree’s shape, you should explain why and give three big-O expressions: one for the best case, one for the worst case if the tree is balanced, and one for the worst case if the tree is not balanced. If the time efficiency does not depend on the keys or the shape of the tree, you should explain why and give one big-O expression.

2. If the tree is a binary search tree, we can revise the algorithm to take advantage of the ways in which the keys are arranged in the tree. Write a revised version of anyGreaterInTree that does so. Your new method should avoid visiting nodes unnecessarily. In the same way that the search for a key doesn’t consider every node in the tree, your method should avoid considering subtrees that aren’t needed to determine the correct return value. Like the original version of the method above, your revised method should also be recursive.

   Note: In the files that we’ve given you for Part II, the LinkedTree class includes the methods shown above. Feel free to replace the original anyGreaterInTree() method with your new version so that you can test its correctness. However, your new version of the method should ultimately be included in your copy of ps8_partI.

3. For a binary search tree with n nodes, what is the time efficiency of your revised algorithm as a function of n?

   Here again, if the time efficiency depends on the keys in the tree or on the tree’s shape, you should explain why and give three big-O expressions: one for the best case, one for the worst case if the tree is balanced, and one for the worst case if the tree is not balanced. If the time efficiency does not depend on the keys or the shape of the tree, you should explain why and give one big-O expression.

Problem 2: Balanced search trees

6 points; individual-only

Illustrate the process of inserting the key sequence

V, C, M, F, K, H, P, Y, S, J

into an initially empty 2-3 tree. Show the tree after each insertion that causes a split of one or more nodes, and the final tree.

We have given you a sample diagram that includes nodes of different sizes. Make copies of the diagram so that you can use separate diagrams for the results of each insertion that causes a split, and for the final tree. Note that you do not need to keep the shape of the tree that we have given you. Rather, you should edit it as needed: deleting or adding nodes and edges, replacing the Xs with keys, adding or removing keys, and making whatever other changes are needed.

Problem 3: Hash tables

10 points total; individual-only

We will finish the material needed for this problem during the week of April 25.

The following sequence of keys is to be inserted into an initially empty hash table of size 8:

to, the, their, my, bring, do, a, you, go

The hash function assigns to each key the number of characters in the key. For example, h("the") is 3, because "the" has 3 characters.

1. Assume that linear probing is used to insert the keys. Specify which key causes overflow, and show the table at that point by adding the keys at the appropriate positions in the table that we have provided for 3-1 in ps8_partI.

2. Now assume that quadratic probing is used. Specify which key causes overflow, and show the table at that point.

3. Finally, assume that double hashing is used, and that the second hash function h2 is based on the part of speech of the key, as follows:

   • h2(k) = 2 if k is an article (e.g., "the", "a")
   • h2(k) = 3 if k is a verb (e.g., "bring", "do", "go")
   • h2(k) = 4 if k is a noun or pronoun (e.g., "their", "my", "you")
   • h2(k) = 5 if k is any other part of speech ("to").

   Specify which key causes overflow, and show the table at that point.

Now consider the fourth table provided for this problem in ps8_partI (the one under section 3-5). Assume that this hash table is using double hashing with the hash functions described above. The table includes a number of existing keys, and positions 1 and 4 are shaded to indicate that they are removed positions – i.e., ones that used to hold an item that has since been removed.

4. If we now insert an item whose key is "try" (which is a verb), what is the probe sequence – i.e., the sequence of positions examined during probing – for that insertion?

5. Show what the table will look like after "try" is inserted.

Problem 4: Complete trees and arrays

6 points total; individual-only

We will cover the material needed for this problem during the week of April 25.

Assume that you have a complete tree with 112 nodes, and that you represent it in array form.

1. Node A of the tree is in position 40 of the array. What are the indices of A’s left child, right child, and parent? Explain how you got your answers.

2. What is the height of the tree? Explain your answer briefly.

3. The bottom level of the tree contains some number of leaf nodes. Is the rightmost leaf node in the bottom level the left child of its parent or the right child of its parent? Explain your answer briefly.

Problem 5: Heaps

8 points total; individual-only

We will cover the material needed for this problem during the week of April 25.

Consider the following heap of integers:

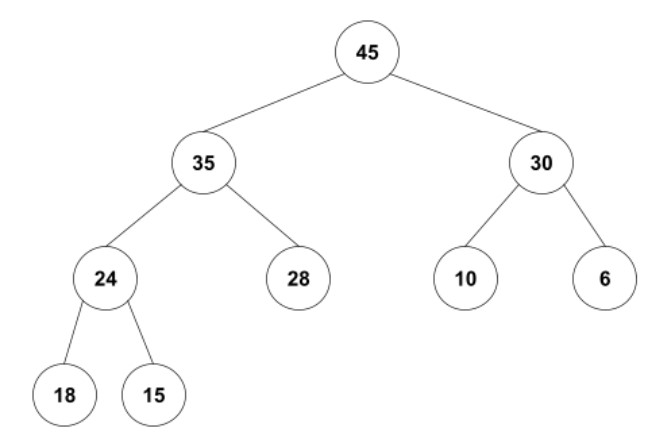
1. Show the heap as it will appear:

   • after one removal (i.e., after one call to the remove() method discussed in lecture)

   • after a second removal.

   You should include two separate diagrams, one for how the heap will look after each removal. To do so, you should:

   • Edit the diagram provided in section 5-1 of ps8_partI by clicking on it and then clicking the Edit link that appears below the diagram.

   • Make the necessary changes to the tree to show the results of the first removal.

   • Click the Save & Close button.

   • Make a copy of your edited diagram within the Google Doc and edit it to show the results of the second removal.

2. Suppose we have the original heap and that we insert the following sequence of values:

   40, 55, 20
   

   Show the final heap by editing the diagram that we have provided in section 5-2 of ps8_partI.

Submitting your work for Part I

Note: There are separate instructions at the end of Part II that you should use when submitting your work for that part of the assignment.

Submit your ps8_partI.pdf file using these steps:

1. If you still need to create a PDF file, open your ps8_partI file on Google Drive, choose File->Download->PDF document, and save the PDF file in your ps8 folder.

2. Login to Gradescope by clicking the link in the left-hand navigation bar, and click on the box for CS 112.

3. Click on the name of the assignment (PS 8: Part I) in the list of assignments on Gradescope. You should see a pop-up window labeled Submit Assignment. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

4. Choose the Submit PDF option, and then click the Select PDF button and find the PDF file that you created. Then click the Upload PDF button.

5. You should see a question outline along with thumbnails of the pages from your uploaded PDF. For each question in the outline:

   • Click the title of the question.
   • Click the page(s) on which your work for that question can be found.

   As you do so, click on the magnifying glass icon for each page and doublecheck that the pages that you see contain the work that you want us to grade.

6. Once you have assigned pages to all of the questions in the question outline, click the Submit button in the lower-right corner of the window. You should see a box saying that your submission was successful.

Part II

60 points total

Preparing for Part II

Begin by downloading the following zip file: ps8.zip

Unzip this archive, and you should find a folder named ps8, and within it the files you will need for Part II.

Keep all of the files in the ps8 folder, and open that folder in VS Code using the File->Open Folder or File->Open menu option.

Problem 6: Binary tree iterator

25 points; pair-optional

This is the only problem of the assignment that you may complete with a partner. See the rules for working with a partner on pair-optional problems for details about how this type of collaboration must be structured.

The traversal methods that are part of the LinkedTree class are limited in two significant ways: (1) they always traverse the entire tree; and (2) the only functionality that they support is printing the keys in the nodes. Ideally, we would like to allow the users of the class to traverse only a portion of the tree, and to perform different types of functionality during the traversal. For example, users might want to compute the sum of all of the keys in the tree. In this problem, you will add support for more flexible tree traversals by implementing an iterator for our LinkedTree class.

You should use an inner class to implement the iterator, and it should implement the following interface:

public interface LinkedTreeIterator {
    // Are there other nodes to see in this traversal?
    boolean hasNext();

    // Return the value of the key in the next node in the
    // traversal, and advance the position of the iterator.
    int next();
}

There are a number of types of binary-tree iterators that we could implement. We have given you the implementation of a preorder iterator (the inner class PreorderIterator), and you will implement an inorder iterator for this problem.

Your inorder iterator class should implement the hasNext() and next() methods so that, given a reference named tree to an arbitrary LinkedTree object, the following code will perform a complete inorder traversal of the corresponding tree:

LinkedTreeIterator iter = tree.inorderIterator();
while (iter.hasNext()) {
    int key = iter.next();

    // do something with key
}

Here are the tasks that you should perform:

0. Review the code that we’ve given you in the PreorderIterator class and the preorderIterator() method, and understand how that iterator works. It’s worth noting that you can’t actually use a PreorderIterator object yet, because it will only work after you have completed the next task.

   We reviewed the PreorderIterator class in Lab 12. In addition, we have created an overview of that class that we encourage you to read.

1. In order for an iterator to work, it’s necessary for each node to maintain a reference to its parent in the tree. These parent references will allow the iterator to work its way back up the tree.

   In the copy of LinkedTree.java that we’ve given you for this assignment, the inner Node class includes a field called parent, but the LinkedTree code does not actually maintain this field as the tree is updated over time. Rather, this parent field is assigned a value of null by the Node constructor, and its value remains null forever.

   Before implementing the iterator, you should make whatever changes are needed to the existing LinkedTree methods so that they correctly maintain the parent fields in the Node objects.

   • For example, when a Node object is first inserted in the tree, you should set its parent field to point to the appropriate parent node.

   • Think about when the parent of a node can change, and update the necessary method(s) to modify the parent field in a Node object whenever its parent changes.

   • The root of the entire tree should have a parent value of null.

2. Next, add a skeleton for your iterator class, which you should name InorderIterator (note that only the two Is are capitalized). It should be a private inner class of the LinkedTree class, and it should implement the LinkedTreeIterator interface. Include whatever private fields will be needed to keep track of the location of the iterator. Use our PreorderIterator class as a model.

3. Implement the constructor for your iterator class. Make sure that it performs whatever initialization is necessary to prepare for the initial calls to hasNext() and next().

   In the PreorderIterator constructor that we’ve given you, this initialization is easy, because the first node that a preorder iterator visits is the root of the tree as a whole. For an inorder iterator, however, the first node visited is not necessarily the root of the tree as a whole, and thus you will need to perform whatever steps are needed to find the first node that the inorder iterator should visit, and initialize the iterator’s field(s) accordingly.

4. Implement the hasNext() method in your iterator class. Remember that it should execute in O(1) time.

5. Implement the next() method in your iterator class. Make sure that it includes support for situations in which it is necessary to follow one or more parent links back up the tree, as well as situations in which there are no additional nodes to visit. If the user calls the next() method when there are no remaining nodes to visit, the method should throw a NoSuchElementException.

6. Add an inorderIterator() method to the outer LinkedTree class. It should take no parameters, and it should have a return type of LinkedTreeIterator. It should create and return an instance of your new class.

7. Test everything! At a minimum, you must do the following: In the main() method, add a unit test that uses the while-loop template shown near the start of this problem to perform a full inorder traversal of a sample tree.

Problem 7: Implementing a hash table using separate chaining

35 points; individual-only

In lecture, we discussed the following interface for a hash table ADT:

public interface HashTable {
    boolean insert(Object key, Object value);
    Queue<Object> search(Object key);
    Queue<Object> remove(Object key);
}

We also examined one implementation of this interface that uses open addressing (the OpenHashTable class that we’ve included in the ps8 folder).

In this problem, you will complete another implementation of this interface – one that uses separate chaining instead of open addressing. Its class will be called ChainedHashTable.

We have given you a skeleton for this class in the ps8 folder. It includes two private fields:

• one called numKeys for the number of keys in the hash table

• one called table that holds a reference to the array that you will use for the hash table. However, rather than having each element of the array store a single entry as we do in open addressing, each element of the array must serve as a bucket or chain of entries.

We have given you a private inner class called Node for the nodes in each chain. Each element of the table array must hold a reference to the first node in its linked list of nodes, and you will need to create and manipulate these nodes within your hash table methods.

Each Node object has fields that allow it to store:

• a single key

• the collection of values associated with that key, using an instance of our LLQueue class

• a reference to the next node in the linked list (if any).

We have also given you:

• a copy the h1() method from our OpenHashTable class, which you must use as the hash function of your implementation (Note: Because separate chaining allows all entries whose keys are hashed to a given position in the table to stay in that position, you will not need to perform any probing. As a result, you won’t need the second hash function h2() from OpenHashTable.)

• a toString() method that will allow you to see the current contents of the table. It returns a string of the form

  [table[0], table[1], ..., table[size - 1]]
  

  where each position of the table is represented by either:

  • the key or keys in that position’s chain of entries, separated by semi-colons and surrounded by curly braces.

  • the word null if there are no keys in that position.

Your tasks

1. Review all of the provided code, and make sure that you understand it.

2. Add a constructor that takes the size of the hash table as its only parameter and initializes the hash table accordingly. It should throw an IllegalArgumentException if the size is not positive.

3. Implement each method from the HashTable interface as efficiently as possible. Make sure that each of these methods has the same basic functionality as the corresponding method from the OpenHashTable class discussed in lecture. In particular, they should throw exceptions for the same reasons that the OpenHashTable methods do.

   As you add or remove items from the table, make sure that you update numKeys accordingly.

   Because a given chain can grow to an arbitrary length, the hash table will never overflow, and thus your insert method can always return true.

   For example, if you run this test code:

   ChainedHashTable table = new ChainedHashTable(5);
   table.insert("howdy", 15);
   table.insert("goodbye", 10);
   System.out.println(table.insert("apple", 5));
   System.out.println(table);
   

   you should see:

   true
   [{apple; howdy}, null, null, {goodbye}, null]
   

   Note that:

   • Position 0 has a chain with two keys, because both "howdy" and "apple" are assigned a hash code of 0 by h1() when the table size is 5.

   • Position 3 has a chain with one key, because "goodbye" is assigned a hash code of 3 by h1() when the table size is 5.

4. Define an accessor method for the number of keys. Call this method getNumKeys(). For example, this test code:

   ChainedHashTable table = new ChainedHashTable(5);
   table.insert("howdy", 15);
   table.insert("goodbye", 10);
   table.insert("apple", 5);
   System.out.println(table.getNumKeys());
   table.insert("howdy", 25);     // insert a duplicate
   System.out.println(table.getNumKeys());
   

   should print:

   3
   3
   

   because inserting a duplicate does not change the number of keys.

5. Although a hash table that uses separate chaining won’t overflow, it can become too full to offer decent performance. To allow clients to measure the degree of fullness, add a method called load() that takes no parameters and that returns a value of type double that represents the load factor of the table: the number of keys in the table divided by the size of the table.

   For example, this test code:

   ChainedHashTable table = new ChainedHashTable(5);
   table.insert("howdy", 15);
   table.insert("goodbye", 10);
   table.insert("apple", 5);
   System.out.println(table.load());
   table.insert("pear", 6);
   System.out.println(table.load());
   

   should print:

   0.6
   0.8
   

6. To allow clients to obtain all of the keys in the hash table, add a method called getAllKeys() that takes no parameters and that returns an array of type Object containing all of the keys in the hash table.

   For example, the following test code:

   import java.util.*;
   ChainedHashTable table = new ChainedHashTable(5);
   table.insert("howdy", 15);
   table.insert("goodbye", 10);
   table.insert("apple", 5);
   table.insert("howdy", 25);    // insert a duplicate
   Object[] keys = table.getAllKeys();
   System.out.println(Arrays.toString(keys));
   

   should print:

   [apple, howdy, goodbye]
   

7. To deal with situations in which the table becomes too full, add a method called resize() that takes an integer representing the new size, and that grows the table to have that new size. It should not return a value.

   As discussed in lecture, it is not possible to simply copy every element of the current table into a new, larger table. This is because a given key may belong in a different position in the larger table. As a result, you will need to rehash the current keys in the hash table to ensure that they end up in the correct position in the resized table.

   For example, the following test code:

   ChainedHashTable table = new ChainedHashTable(5);
   table.insert("howdy", 15);
   table.insert("goodbye", 10);
   table.insert("apple", 5);
   System.out.println(table);
   table.resize(7);
   System.out.println(table);
   

   should print:

   [{apple; howdy}, null, null, {goodbye}, null]
   [null, {apple}, null, null, null, {howdy}, {goodbye}]
   

   Note that in this case, resizing the table causes all three keys to end up in different positions!

   Special cases:

   • The method should throw an IllegalArgumentException if the specified new size is less than the table’s current size.

   • If the specified new size is the same as the table’s current size, the method should return without doing anything.

8. Add a main() method that performs at least two unit tests for each of the methods in the class. Use the same unit-test format that we specified in Problem 8 of Problem Set 7.

Submitting your work for Part II

Note: There are separate instructions at the end of Part I that you should use when submitting your work for that part of the assignment.

You should submit only the following files:

• LinkedTree.java
• ChainedHashTable.java

Make sure that you do not try to submit a .class file or a file with a ~ character at the end of its name.

Here are the steps:

1. Login to Gradescope as needed by clicking the link in the left-hand navigation bar, and then click on the box for CS 112.

2. Click on the name of the assignment (PS 8: Part II) in the list of assignments. You should see a pop-up window with a box labeled DRAG & DROP. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

3. Add your files to the box labeled DRAG & DROP. You can either drag and drop the files from their folder into the box, or you can click on the box itself and browse for the files.

4. Click the Upload button.

5. You should see a box saying that your submission was successful. Click the (x) button to close that box.

6. The Autograder will perform some tests on your files. Once it is done, check the results to ensure that the tests were passed. If one or more of the tests did not pass, the name of that test will be in red, and there should be a message describing the failure. Based on those messages, make any necessary changes. Feel free to ask a staff member for help.

   Note: You will not see a complete Autograder score when you submit. That is because additional tests for at least some of the problems will be run later, after the final deadline for the submission has passed. For such problems, it is important to realize that passing all of the initial tests does not necessarily mean that you will ultimately get full credit on the problem. You should always run your own tests to convince yourself that the logic of your solutions is correct.

7. If needed, use the Resubmit button at the bottom of the page to resubmit your work. Important: Every time that you make a submission, you should submit all of the files for that Gradescope assignment, even if some of them have not changed since your last submission.

8. Near the top of the page, click on the box labeled Code. Then click on the name of each file to view its contents. Check to make sure that the files contain the code that you want us to grade.