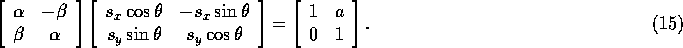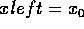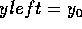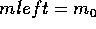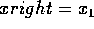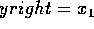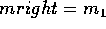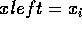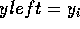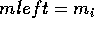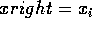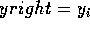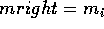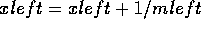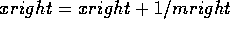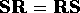 , only if
, only if 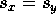 ,
or
,
or 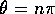 for integer values of n. Start by multiplying the matrices:
for integer values of n. Start by multiplying the matrices:
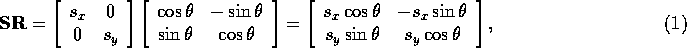
and
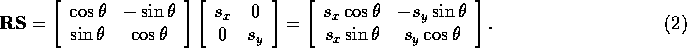
If 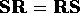 , then clearly
, then clearly
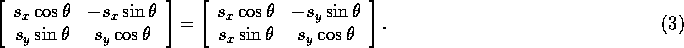
Note that the diagonal elements of both matrices are the same, while the off-diagonal elements are different. This means that for the matrices to be equal, it must be the case that
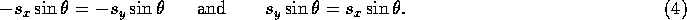
This will be true when 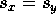 , or when
, or when 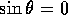 (which happens only when
(which happens only when
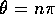 for integer values of n). Otherwise, the off diagonal elements of the
matrices will not be equal, and therefore
for integer values of n). Otherwise, the off diagonal elements of the
matrices will not be equal, and therefore 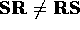 .
.
The homogeneous coordinate representation is more convenient here because we need to include translation in our formulation. Thus we can build a general reflection about a line as a concatenation of linear transforms. We begin by translating to the line's y intercept to the origin using a translation matrix:

We then need to rotate the line to align it with the x axis:

The sine and cosine for alignment can be found directly from the line equation:
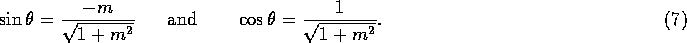
Now that we have a way to get between the line's coordinate system and the world coordinate system, we can employ reflection about the x-axis:

We then inverse rotate, back into the line's orientation:

And finally, translate from the origin back to the line's y intercept:

Thus we build our arbitrary reflection as a concatenation of transforms. We first align the coordinate system of the line with the x axis, we then reflect, and then we return to the original coordinate system:

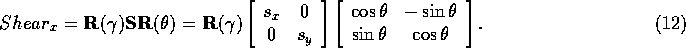
Multiplying out 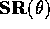 we get
we get

We want to find 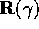 that rotates
that rotates
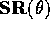 into the x shear matrix:
into the x shear matrix:

In general, multiplying by a rotation matrix takes the form:
The lower left corner of the resulting shear matrix must satisfy
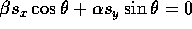 . This means that
. This means that
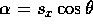 and
and 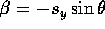 .
Therefore the angle for the second rotation matrix is
.
Therefore the angle for the second rotation matrix is  , and we
need to scale the whole system by
, and we
need to scale the whole system by 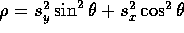 . We can now rewrite in terms of this rotation and scaling:
. We can now rewrite in terms of this rotation and scaling:
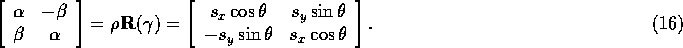
Plugging into Equation 15 and multiplying out, we get:
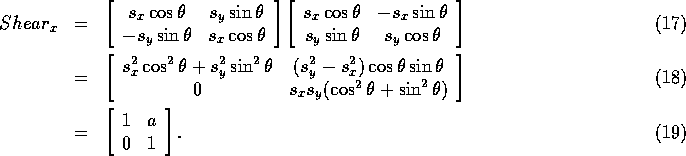
This gives us the equations:
From Equation 22, we see that 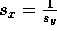 .
By plugging this into Equation 20, we find that
.
By plugging this into Equation 20, we find that

This holds true when 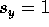 or
or 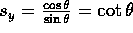 . We prefer
the case when
. We prefer
the case when 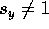 , and plug into Equation 21:
, and plug into Equation 21:
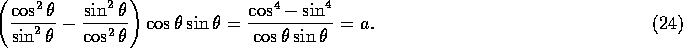
Using trigonometric identities, we find that

This means that

In summary, the x direction shear matrix can be written:

where

discard horizontal edgessort remaining edges into a table using lower end point
(sort by increasing y, and then increasing x)
find ymin and ymax for the quadrilateral
for each edge i in the table
find, the maximum y value for the edge
find, the x value at the edge's lower end point
find the slopefor the edge
end
i=2for y=ymin; y < ymax; y = y+1 do
for x=xleft; x<=xright; x = x+1
write_pixel(x,y,color)
if yleft == y then replace left edge with next active edge
i = i+1
end
if yright == y then replace right edge with next active edge
i=i+1
end
endfor x=xleft; x<=xright; x = x+1
write_pixel(x,ymax,color)
Stan Sclaroff
Created: February 20, 1995